Integrais duplas sobre regiões gerais
Calcule a integral dupla
Em que é a região plana:
Passo 1
Para resolver essa integral, precisamos saber os limites de integração! Para isso, vamos dar uma olhada na região ?
As desigualdades nos dizem que e são maiores ou iguais a , e que , ou seja, é menor ou igual a reta . Juntando tudo temos:
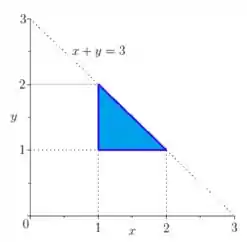
Para interpretar essas desigualdades é legal colocar o dedo sobre a curva e ver o que temos: colocando o dedo sobre a reta, deve ser menor do que ela, então andamos para baixo dela! E, como e são maiores ou iguais a , estamos em cima de e a direita de ;)
Passo 2
Agora, podemos ver os limites de integração da integral dupla! Como a reta é , temos que é função de , logo, devemos integrar antes em relação a . Além disso, vemos que Como quando temos (vértice direito do triângulo), temos que . Colocando esses limites na integral, fica:
Passo 3
Pronto! Agora só precisamos resolver a integral ;) Veja que o que temos é:
E, integrando em relação a , temos:
Dando aquela ajeitada, temos:
Agora, integrando em relação a , temos:
Pronto! Integral resolvida!