Se é um triângulo de vértices (0,0), (2,0) e (0,2) então o valor da integral é:
Passo 1
Pra resolver essa vamos começar vendo essa região que ele chamou de .
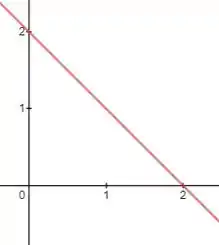
Pra a gente pode escrever isso, é importante que a gente conheça a função que descreve aquela reta ali em cima. Ou seja, isso mesmo, vamos descobrir a equação da reta. Daí é contigo...cada um faz do jeito que acha melhor. Eu particularmente acho mais tranquilo de fazer por determinantes.
Com isso a gente já tem a equação da reta. Agora, eu vou isolar o x, uma vez que a questão pediu pra gente integram dx e depois dy, show? (só falei isso pq no enunciado ele escreveu a integral desse jeito mas não faz diferença nenhuma se você calcula como uma integral do tipo 1 ou 2)
Bom, agora falta só a gente montar a integral e resolver.
Passo 2
A integral, no final das contas vai ficar