UFF, Volta Redonda, Cálculo Diferencial e Integral II, P2 - 2018.2, Questão 1a.
1 – Considere a integral abaixo
a) esboce a região descrita nos limites de integração.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão nosso objetivo é obter graficamente a região de integração da integral
Lembra como fazemos isso? 😎
Ao calcular uma integral dupla, os limites de integração da direita para a esquerda, são relacionadas as variáveis de integração da esquerda para a direita, ou seja, nesse caso, e são os limites de integração de e e de .
Entendeu até aqui? 👀
Passo 2
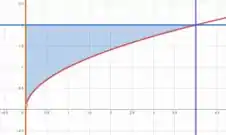
O que estamos fazendo ao calcular uma integral, é calcular a área abaixo da função entre e para e entre e para .
Em outras palavras, entre e e entre e .
Plotando essas curvas no plano cartesiano, temos
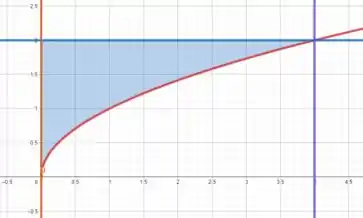
Portanto, a área hachurada entre as curvas é chamada de região de integração para esse caso
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
