Considere uma lâmina que ocupa a região planar que se encontra entre a reta e a parábola . Suponha que a densidade em um ponto qualquer na lâmina seja dada pela função . Determine a massa total da lâmina.
Passo 1
Cara, vamos esboçar essa região, para ter uma ideia da cara dela, tá?
Para esboçar essa região, precisamos esboçar essas curvas no plano . Vamos pensar em cada uma delas:
- é uma reta que passa pela origem, com inclinação de .
- é uma parábola que passa pela origem. Mas repara que quem está elevado ao quadrado é o . Então nossa parábola está com a concavidade virada para a parte crescente de , e não de , como .
Colocando tudo no mesmo gráfico e marcando a região limitada ao mesmo tempo por essas duas curvas, achamos
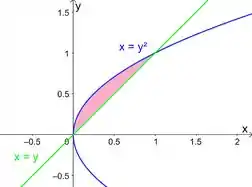
Passo 2
Podemos calcular a massa dela lâmina montando uma integral dupla com integrando igual a sua densidade .
Aí a gente precisa limitar e para descrever essa região que a gente esboçou. Vamos descrever ela como uma região do tipo , já que temos funções de
Vemos que no eixo , nossa região está entre e a outra interseção dessas duas curvas, que podemos achar igualando suas expressões
Daí a gente tira que
E no eixo , ela está entre a funçõe (limitando inferiormente, ou seja, pela esquerda) e (limitando superiormente, ou seja, pela direita):
Esses vão ser nossos extremos de integração. E vamos integrar primeiro em relação a , porque essa variável está limitada entre funções.
Fica assim:
Passo 3
Agora é calcular essa belezura:
Vamos calcular cada uma dessas integrais separadamente. A primeira é um produto entre duas funções simples, aí a gente usa a integração por partes:
Lembrando da regrinha LIATE, vamos escolher como nosso , e o que sobrar como :
Aí a gente substitui isso na fórmulinha
Passo 4
A última integral a gente calcula com a substituição simples
Nossos novos extremos de integração ficam
E a integral fica
Voltando para a nossa massa e substituindo que a gente achou
Prontinho!