USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista - Integrais Duplas e Teorema de Fubini, Questão 2
Desenhe a região de integração no plano e calcule a integral iterada
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos o resultado da seguinte integral dupla:
Para podermos resolver isso, devemos resolver uma integral de cada vez.
Além disso, a questão também nos pede para desenhar a região de integração.
Não entendeu? Então bora junto 😉
Passo 2
Bom... resolvendo a integral dupla:
Fazendo e, portanto, , temos:
Passo 3
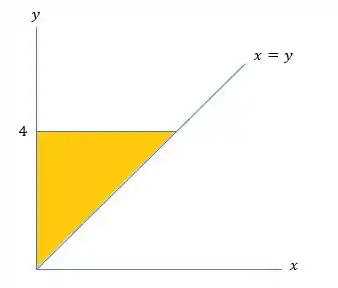
Nesse sentido, desenhando a região de integração, encontramos a seguinte figura:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x