UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 1, Questão 1e
Exercício 1. Calcule
(e)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, queremos calcular a integral dupla de com variando de a e variando de a .
Tem ideia de como fazer isso? 😉
Para calcular uma integral dupla de uma função , observamos a ordem de integração, caso tenhamos primeiro integramos com relação a e dois com relação a . Se for o contrário , primeiro integramos em e depois em .
Já os limites de integração podem ser interpretados como os meios com os meios e os extremos com os extremos...
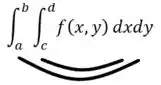
Onde e , por exemplo.
Sacou? Bora começar! 😬
Passo 2
Nesse caso, temos
Integrando com relação a pelo método de substituição fazendo e
Voltando para
Aplicando os limites de integração...
Integrando o resultado em função de pelo mesmo método
Aplicando os limites de integração
Fim! Iae, o que achou? Responde Aí! 😁
