Responda os itens a seguir.
(a) Sejam e funções integráveis em uma região limitada do plano. Se para todo qual a relação entre e ?
(Obs: não precisa justificar a relação)
(b) Use a relação do item (a) para mostrar que
onde é a região delimitada pelas retas
Passo 1
a) Se podemos automaticamente afirmar que
Passo 2
b) Observe que para o caso do seno, sabemos que ele varia entre 1 e -1, certo?
Para o caso daquestão então, ficamos com
Como nosso seno está elevada a quarta, não teremos parte negativa, então ficamos com:
Mas no caso da nossa questão existe ainda um +1, certo? Então vamos somar 1 em todas as partes da igualdade.
Ficamos por fim então com:
Passo 3
Agora o que nós precisamos então é calcular essa integral.
A região D nos é dada pelo enunciado como sendo delimitada pelas retas ou seja:
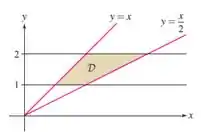
Por essa imagem conseguimos ver com mais clareza que temos y variando entre 1 e 2, e x variando entre as retas, x=y e . Montando a integral então ficamos com:
Com isso obtemos então que :
Resposta
Ei, a resposta está no passo a passo :)