Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 421234567891011121314151617181920212223242526272829303132333435363738394041434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 2c

Calcule

∫ ∫ R x 2 y 2 d A

, onde R é a porção limitada do primeiro quadrante que está entre as duas hipérboles x y   =   1   e   x y   =   2   e as duas retas y   =   x   e   y   =   4 x .

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de cálculo 2. Queremos

∫ ∫ R x 2 y 2 d A

onde R é a porção limitada do primeiro quadrante que está entre as duas hipérboles x y   =   1   e   x y   =   2   e as duas retas y   =   x   e   y   =   4 x .

A primeira coisa que vamos fazer é desenhar nossa região de interesse

Passo 2

Nossa região é

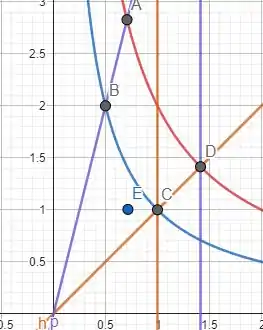
Note que ela já está dividida em três partes. de forma que podemos expressar nossa integral como a soma das integrais em cada uma dessas partes. Para isso. Vamos calcular os valores de x dos pontos A e D

Começando por A . Bem, temos que

2 / x = 4 x

⇒ x = 2 / 2

E para D temos

2 / x = x

⇒ x = 2

Dessa forma, podemos reescrever a nossa integral como

∫ ∫ R x 2 y 2 d A = ∫ 1 / 2 2 / 2 ∫ 1 / x 4 x x 2 y 2 d y d x + ∫ 2 / 2 1 ∫ 1 / x 2 / x x 2 y 2 d y d x + ∫ 1 2 ∫ x 2 / x x 2 y 2 d y d x

Passo 3

Vamos resolver

∫ 1 / 2 2 / 2 ∫ 1 / x 4 x x 2 y 2 d y d x + ∫ 2 / 2 1 ∫ 1 / x 2 / x x 2 y 2 d y d x + ∫ 1 2 ∫ x 2 / x x 2 y 2 d y d x

= 1 3 ∫ 1 / 2 2 / 2 x 2 ( ( 4 x ) 3 - ( 1 x ) 3 ) d x + 1 3 ∫ 2 / 2 1 x 2 ( ( 2 / x ) 3 - ( 1 x ) 3 ) d x + 1 3 ∫ 1 2 x 2 ( ( 2 / x ) 3 - ( x ) 3 ) d x

= 1 3 ( 4 ∫ 1 / 2 2 / 2 x 5 d x - ∫ 1 2 x 5 d x   - ∫ 1 / 2 1 x - 1 d x   +   2 ∫ 2 / 2 2 x - 1 d x )

= 1 3 ( 28 / 2 6 6 - 7 / 6   + l o g ( 1 / 2 )   +   2 l o g ( 2 ) )

= 1 3 ( 28 / 2 6 6 - 7 / 6   + l o g ( 2 ) )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x