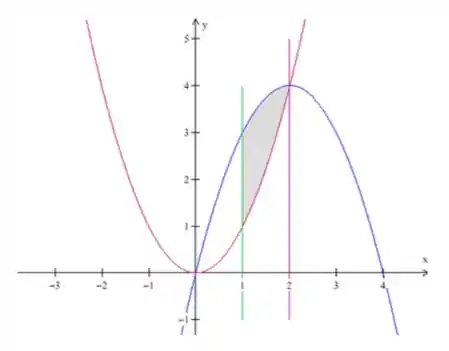
Determine o esboço da região do plano sobre a qual a integral é calculada:
Passo 1
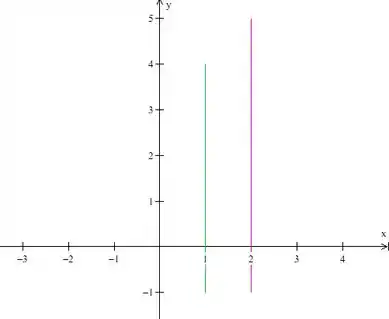
Vamos analisar os intervalos de integração que temos para :
No gráfico, é o seguinte:
Passo 2
Agora para :
Isso quer dizer que temos as curvas e limitando nossa região. A primeira, nós sabemos que é uma parábola com concavidade para cima e que passa pela origem, sem grandes novidades:
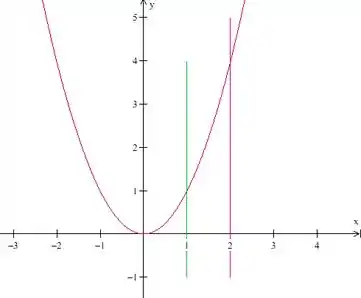
Agora vamos ver a outra curva, .
Como temos de um lado e do outro, sabemos que também é uma parábola, mas repare no sinal negativo de . Isso significa que a concavidade da parábola está voltada para baixo.
E mais: temos esse termo , que significa que ela está deslocada de alguma forma. Vamos calcular suas raízes para entender melhor:
Ela passa então pelos pontos e . Vamos desenhar isso aqui:
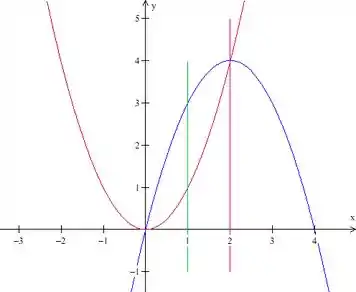
Passo 3
Agora vamos identificar a região:
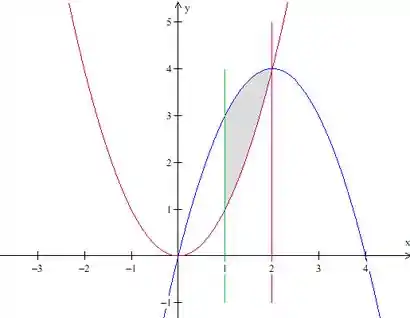
Beleza? Tranquilo, né?
Resposta