Use integral dupla para calcular a área da região limitada por:
No primeiro quadrante.
Passo 1
A gente sabe que a área da região a gente faz pela integral dupla:
Fazendo um esboço da nossa região, nós temos duas retas: ; e um gráfico mais estranho: . Como ele só quer a parte no primeiro quadrante, temos algo assim:
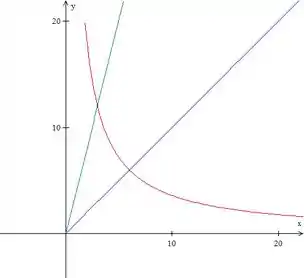
Não dá pra escrever a região nem como tipo , nem como tipo , diretamente, então vamos ter que separar em dois pedaços e , mas calma que não é nada demais, você vai ver...
Passo 2
O primeiro pedaço vai ser até a reta de cima encontrar com a curva. Se igualarmos o vamos ter algo assim:
Então a região é assim:
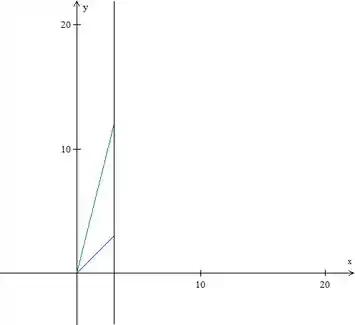
A integral vai assim, então:
Passo 3
Calculando a integral que encontramos no passo anterior:
Agora só falta o outro pedaço!
Passo 4
O pedaço que tava faltando era:
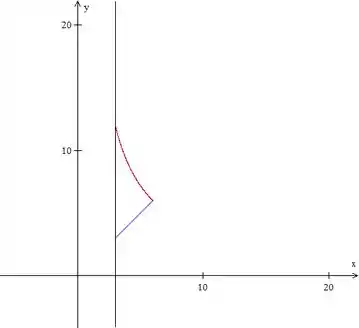
Que também é tipo , então vamos achar o ponto que a reta de baixo encontra a curva:
E a integral fica, então:
Passo 5
Agora é só calcular a integral:
Passo 6
Agora é só somar tudo: