UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 5.
5 - Calcule , onde é o quadrado .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Essa conta parece que vai ser difícil? Relaxa! Ela é bem rapidinha, veja só!
Nessa questão, vamos obter a integral dada pela função trigonométrica no intervalo de integração dado pela região , que é formado por um quadrado que em , varia de a e em também varia de a .
Tá conseguindo visualizar nossa região de integração? Vamos plotar as curvas que limitam nossa região.
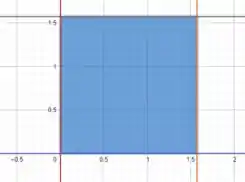
E aí, como vai ficar nossa integral? 🤔
Bora ver.
Passo 2
Como nossa região de integração é um quadrado, é relativamente mais simples obter os limites de integração para e .
Como está variando de a , da maior curva à menor, o limite superior em é e o inferior é .
Com relação a temos o mesmo resultado, como estamos variando de a , os limites de integração em é no superior e no inferior.
Com isso, nossa integral terá a seguinte cara
Primeiro a gente calcula a integral e depois aplicamos os limites de integração.
Integrando em função de , temos
Como não depende de , podemos tirar da integral
Pelo teorema fundamental do cálculo, sabemos que a integral do é , logo
Aplicando os limites de integração, vamos obter
Como e , então
Interessante, não é? 😎
Passo 3
A partir desse resultado, vamos integrar com relação a .
Como acabamos de ver, pelo teorema fundamental do cálculo, a integral do é
Aplicando os limites de integração, temos
e , então
Achou que ia ser complicado?
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
