Calcule
Onde é a região limitada pelas parábolas e .
Passo 1
Primeiramente, vamos fazer um esboço para entender melhor o que está sendo pedido. Como as duas parábolas tem o coeficiente do termo positivos, elas estão viradas para cima. Fazendo , descobriremos suas raízes.
A segunda parábola não possui raízes reais, portanto, não corta o eixo .
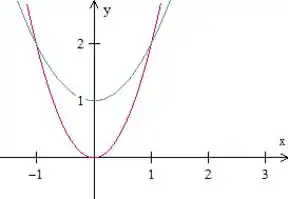
Passo 2
Como essa região está limitada em por duas equações (a parábola vermelha e a azul) e em por 2 números, podemos escrevê-la como do tipo I.
Em teremos:
Para descobrir intervalo em , devemos fazer e interseção entre as equações das parábolas e , encontraremos valores.
Assim, descobrimos que varia entre e (onde as curvas se encontram). Podemos, então, escrever a região como:
Passo 3
Vamos, então, substituir em nossa integral os valores que acabamos de encontrar para o domínio.
Cuidado com a ordem de integração!Lembre-se de que as funções ficam na integral de dentro, enquanto os números ficam na de fora.
Passo 4
Agora vamos integrar em relação a (integral de dentro):
Passo 5
Está na hora, então, de integrar em relação a :