Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 1: Considere as regiões do plano

R 1 = x ,   y ∈ R 2   |   y + 1 - x 2 ≥ 0

R 2 = x ,   y ∈ R 2   |   2 y + x ≤ 1

Seja R = R 1 ∩ R 2 .

d) Considere a integral dupla

I = ∬ R   2 x + 1 2 x + y + 4   d y   d x

Escreva I na forma de uma integral iterada, integrando primeiro com respeito a y e em seguida em relação a x .

Escreva I na forma de uma diferença de integrais simples:

I = ∫ c d h 1 x d x - ∫ c d h 2 x d x

Explicitando c , d , h 1 x e h 2 x .

Obs.: Neste item não é necessário encontrar o valor numérico da I , apenas escrevê-la no formato pedido.

e) Escreva I na forma de uma soma de integrais iteradas, integrando primeiro com respeito a x e em seguida com respeito a y .

Obs.: Neste item não é necessário calcular as integrais.

Passo 1

d)

Para montarmos essa integral aqui integrando primeiro em relação à x e em seguida em relação y , teríamos que descrever a região do TIPO I que é o tip responsável por deixar o x variando entre números:

I = ∬ R   2 x + 1 2 x + y + 4   d y   d x

Mas a gente já fez isso em um dos passos anteriores:

R = x ,   y ∈ R 2   | - 1 + x 2 ≤ y ≤ 1 2 - x 2 ,   - 3 2 ≤ x ≤ 1

Então...

I = ∬ R   2 x + 1 2 x + y + 4   d y   d x =

∫ - 3 2 1 ∫ - 1 + x 2 1 2 - x 2 2 x + 1 2 x + y + 4   d y d x

Passo 2

Para escrever esse mesmo I na forma...

I = ∫ c d h 1 x d x - ∫ c d h 2 x d x

Temos que começar a resolver a integral dupla! Vamos nessa?

I = ∫ - 3 2 1 2 x + 1 ∫ - 1 + x 2 1 2 - x 2 1 2 x + y + 4   d y d x =

Considerando a mudança de variável...

x + y + 4 = t       →

d t = d y

Não se esqueça de trocar os limites de integração também, heim:

y = - 1 + x 2       →         t = x 2 + x + 3

y = 1 2 - x 2       →         t = x 2 + 9 2

Assim...

I = ∫ - 3 2 1 2 x + 1 ∫ - 1 + x 2 1 2 - x 2 1 2 x + y + 4   d y d x = ∫ - 3 2 1 2 x + 1 ∫ x 2 + x + 3 x 2 + 9 2 1 2 t   d t d x =

∫ - 3 2 1 2 x + 1 t x 2 + x + 3 x 2 + 9 2 d x = ∫ - 3 2 1 2 x + 1 x 2 + 9 2 - x 2 + x + 3 d x =

∫ - 3 2 1 2 x + 1 x 2 + 9 2 d x + ∫ - 3 2 1 - 2 x + 1 x 2 + x + 3 d x

Então veja que:

c = - 3 2         e       d = 1

h 1 = 2 x + 1 x 2 + 9 2               e               h 2 = - 2 x + 1 x 2 + x + 3

Passo 3

e)

Poxa, para fazer esse item (inverter a ordem de integração da integral dupla anterior) temos que reescrever a região R , mas dessa vez tentando coloca-la como uma região do tipo 2 !

Nesse tipo devemos ter o y variando entre números, enquanto o x varia entre uma parede esquerda até uma parede direita:

R : a ≤ y ≤ b P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   d i r e i t a    

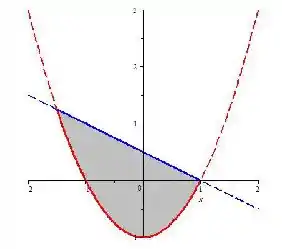
Eu quero que você perceba que a parede esquerda da região muda no ponto em y = 0 , pois em cima ela é a reta 2 y + x = 1 , enquanto que embaixo ela é a parábola y + 1 - x 2 = 0 , então vamos ter que desmembrar a descrição em duas partes: uma com o y abaixo de 0 e outra com o y acima...

R : a ≤ y ≤ b P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   d i r e i t a = a ≤ y ≤ 0 P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   ( r e t a ) 0 ≤ y ≤ b P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   ( p a r a b )

Passo 4

Vamos começar com a descrição da parte de baixo:

a ≤ y ≤ 0 P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   ( r e t a )

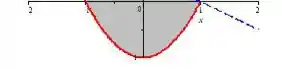
Quem é a ? Sim, é o menor valor que y assume e que no caso é - 1 . A parede esquerda e a direita é a parábola:

y + 1 - x 2 = 0     →         x 2 = y + 1     →

x = ± y + 1

Então, no caso...

a ≤ y ≤ 0 P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   r e t a   →

- 1 ≤ y ≤ 0 - y + 1 ≤ x ≤ y + 1

Passo 5

Agora vamos descrever a parte de cima:

0 ≤ y ≤ b P a r e d e   e s q u e r d a ≤ x ≤ P a r e d e   p a r a b   →

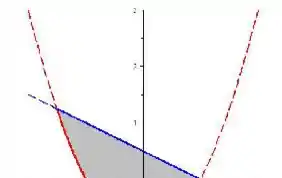
A parede esquerda continua sendo a parábola:

x = - y + 1

Enquanto a parede direita é agora a reta:

2 y + x = 1

O ponto b , por sua vez é a altura máxima da região e ela acontece quando o x = - 3 2 ...

2 y + x = 1   →       2 y - 3 2 = 1   →

y = 5 4

Logo...

0 ≤ y ≤ 5 4 - y + 1 ≤ x ≤ 1 - 2 y

Passo 6

Podemos concluir então que a região é...

R : - 1 ≤ y ≤ 0 - y + 1 ≤ x ≤ y + 1 0 ≤ y ≤ 5 4 - y + 1 ≤ x ≤ 1 - 2 y

Remontando a integral então...

I = ∬ R   2 x + 1 2 x + y + 4   d y   d x =

∫ - 1 0 ∫ - y + 1 y + 1 2 x + 1 2 x + y + 4   d x d y + ∫ 0 5 4 ∫ - y + 1 1 - 2 y 2 x + 1 2 x + y + 4   d x d y

Resposta

Letra d)

I = ∫ - 3 2 1 ∫ - 1 + x 2 1 2 - x 2 2 x + 1 2 x + y + 4   d y d x

I = ∫ - 3 2 1 2 x + 1 x 2 + 9 2 d x + ∫ - 3 2 1 - 2 x + 1 x 2 + x + 3 d x

Letra e)

I = ∫ - 1 0 ∫ - y + 1 y + 1 2 x + 1 2 x + y + 4   d x d y + ∫ 0 5 4 ∫ - y + 1 1 - 2 y 2 x + 1 2 x + y + 4   d x d y

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x