Unicamp, Cálculo 2- P2- 2019.1, questão 4
- Calcule a integral dupla da função sobre a região triangular de vértices .
- A integral acima expressa o volume de qual sólido?
Passo 1
Opa! Tudo bem?
- Pra começar, vamos dar uma olhada na região...
- A integral calculada representa o volume de uma pirâmide de base quadrada, medindo de lado e de altura. Veja só:
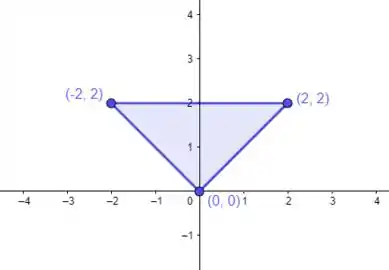
Veja então que:
Já o começa na reta que passa por e sai em na reta que passa por: e . Vamos escrever essas retas então...
Passo 2
Uma reta tem a forma:
Pra reta que passa por , temos:
Escolhendo o ponto , temos a reta:
A outra reta:
A reta é:
E daí temos que os limites de são:
Passo 3
Montando a integral então temos:
Integrando em ...
E calculamos a integral!
Passo 4
E acabamos por aqui!
Resposta
- Pirâmide de base quadrada, lado 4 e altura 2.
Exercícios de Livros Relacionados
Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x