Quarta Questão: Calcule a integral.
onde é a região triangular com vértices , .
Passo 1
Pois bem! Em problemas como esse devemos sempre começar fazendo um esboço da região. Mas não se preocupe, pois fazer isso significa colocar no plano todas os pontos dados e desenhar o triângulo !
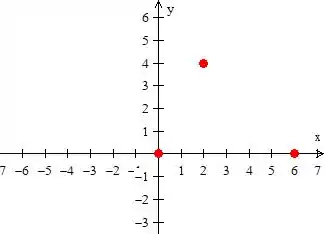
O legal é que já dá pra ver que região estamos trabalhando! :D
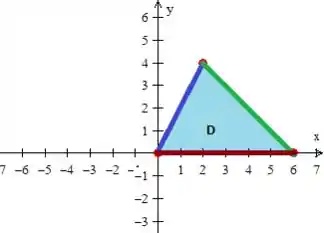
Agora temos que descrever essa região! Bora?
Passo 2
Agora precisamos pensar um pouco: que tipo de descrição podemos fazer de forma que simplifique os cálculos? Do tipo ou do tipo ?
Bem, se fossemos colocar como do tipo , o estaria variando entre na primeira na primeira metade do triângulo entre duas retas...
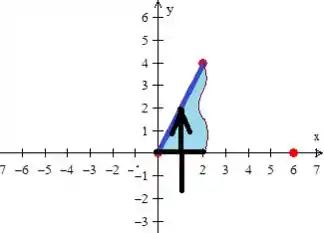
e na segunda, entre outras diferentes duas retas
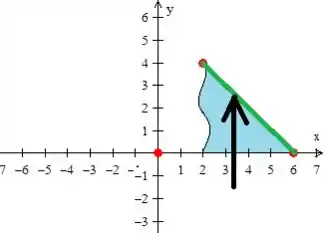
Então teríamos que editar duas integrais duplas. Um trabalhão, neh?
Por isso devemos escolher o Tipo 2, pois assim, colocamos o variando em um intervalo numérico bem definido:
enquanto que o varia dessa reta azul, até a verde:
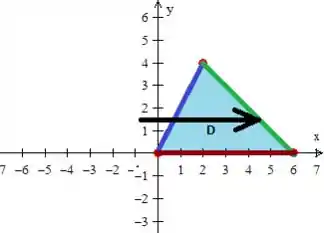
Falta então à gente descobrir quem são essas retas!
Passo 3
Com relação à reta azul primeiro.
Bem, precisamos encontrar a equação da reta dela e cara sabemos que toda reta no plano tem esse formato aqui
No caso, devemos procurar quem é o e quem é o (pra isso, basta substituir os dois pontos que sabemos dela):
Quanto ao ...
logo a reta azul tem equação...
como
isolando o da reta azul ...
Agora bora fazer o mesmo para encontrar a reta verde!
Passo 4
No caso da verde, semelhantemente devemos procurar quem é o e quem é o (substituir os dois pontos que sabemos dela):
Jogando o outro ponto...
Substituindo em...
então
logo a reta verde é tem equação...
como
isolando o da reta verde ...
Passo 5
Com os dois intervalos descobertos
Podemos montar a integral que queremos...
Desmembrando ...
Integrando a de dentro em relação a e, portanto, considerando constante...
Calculando agora a integral de fora...
Essa outra integral pode ser resolvida fazendo uma mudança de variável...
Não esqueça de substituir os limites também, heim!