A massa do conjunto
e
cuja densidade superficial é
é igual a
Escolha uma:
a)
b)
c)
d)
e)
Passo 1
Cara, vamos esboçar essa região, para ter uma ideia da cara dela, tá?
Temos a inequação
A gente pode escrever ela assim
Se ali fosse um sinal de igual, estaríamos falando da reta . Mas como ali diz que é menor que a expressão dessa reta , estamos olhando para o conjunto de valores de menores que a reta.
Assim, a gente está se referindo a toda região abaixo da reta .
Já as outras duas inequações juntas e , nos dizem que nossa região está só no primeiro quadrante, onde as duas variáveis são positivas.
Colocando a região com essas características em um gráfico
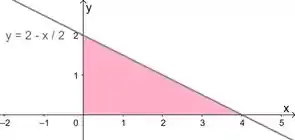
Vamos seguir!
Passo 2
Podemos calcular a massa dela lâmina montando uma integral dupla com integrando igual a sua densidade .
Aí a gente precisa limitar e para descrever essa região que a gente esboçou. Vamos descrever ela como uma região do tipo , já que temos funções de
Vemos que no eixo , nossa região está entre e (sendo essa última a interseção entre a reta inclinada e ). Daí a gente tira que
E no eixo , ela está sendo limita por baixo pela reta e por cima pela reta . Aí temos
Esses vão ser nossos extremos de integração. E vamos integrar primeiro em relação a , porque essa variável está limitada entre funções.
Fica assim:
Passo 3
Agora é calcular essa belezura:
Nessa primeira integral, vai ser constante
Prontinho!
Resposta
Letra b