UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 11.
11 - Determine a área de região delimitada pelas curvas , e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão, vamos calcular a área da região onde é limitada pelas equações , e .
E agora? Como vamos fazer isso?? 🤔
Nesses casos, a primeira coisa que temos que fazer é analisar a região . Se a gente plotar essas curvas no plano, vamos obter o seguinte
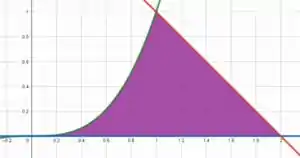
Com isso vemos que nossa área é a região hachurada em roxo. Então você deve pensar que não temos como calcular essa área já que nossa região é um pouco irregular.
Mas temos um truque na manga que chamamos de integral dupla! 🐱👤
Como estamos querendo calcular área, nossa integral vai ser mais ou menos assim.
Vamos começar a calcular nossa integral? 😁
Passo 2
Primeiro temos que definir a variação de e que vão fazer parte dos nossos limites de integração.
Analisando nossa região , vemos que podemos escrever que em (na horizontal) a região varia entre as curvas vermelha e verde, ou seja, entre as curvas e
Isolando em um lado das equações, temos
Como a curva mais distante é a vermelha, logo é nosso limite e é nosso .
Como em já levamos em consideração as curvas, em vamos analisar apenas as constantes.
Observando a região vemos que a altura máxima em é e a mínima é , então e .
Dessa forma, nossa integral será
Primeiro integramos com relação a . Como nossa função de integração é uma constante, nossa integral é essa constante multiplicada pela nossa variável de integração, lembra?
Aplicando os limites de integração
Tranquilo até aqui? 👀
Passo 3
Agora com base no resultado que obtemos integramos com relação a . Nessa integral podemos integrar pelo método de integração polinomial onde somamos no expoente da variável e dividimos a variável pelo resultado dessa soma.
Aplicando os limites de integração, temos
Simplificando um pouco mais, temos
Com isso, a área da nossa região é
Fim! Iae, o que achou? Responde Aí! 😁
