UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV2 - 2022.1, Questão 2
Calcule a integral , onde é a região triangular com vértices , e .
Passo 1
Oiie, tudo certinho com você?
Esta é uma questão de cálculo de volume por integral dupla, temos que o volume desejado é
e a região delimita o nosso volume! Temos que ela é a região triangular com vértices em , e que indica um plano arbitrário! Quando temos uma integral desta forma, podemos escrever o elemento utilizando que
Ou seja, precisamos de uma parametrização! Vamos tentar visualizá-la! Vem comigo!
Passo 2
Temos que estes três vértices geram um plano, e a equação geral do plano é tal que
em que são os componentes do vetor normal ao plano e é obtido conhecendo um ponto pertencente ao plano em questão! Podemos obter o vetor normal construindo dois vetores que pertencem ao plano, por exemplo, os vetores
em que chamei o vértice e o vértice . Da mesma forma, podemos montar o vetor
O vetor normal ao plano pode ser obtido fazendo
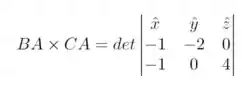
Resolvendo o determinante, temos que
De forma, que a equação do plano deve obedecer
Se usarmos que o ponto pertence ao plano, temos finalmente que
e, portanto, temos que , e a equação do plano é
Vamos utilizar isso para facilitar a nossa parametrização! Bora lá!
Passo 3
Se usarmos então a equação do plano para obter que
Usando que e , temos a seguinte parametrização
Agora precisamos das derivadas parciais
e da mesma forma, podemos obter que
O produto vetorial que precisamos é tal que
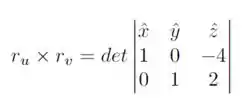
Resolvendo o determinante obtemos que
Que tem como módulo a seguinte expressão
Finalmente, podemos escrever a nossa integral como
Ainda precisamos ver quais são os limites de integração! Vamos fazer isso agora!
Passo 4
A nossa superfície é delimitada pelo plano
obtido através dos três vértices , e . E, temos a seguinte parametrização
Se escolhermos integrar primeiro em , temos os limites dados pelos valores de que vão de à . No entanto, para a integral de dentro devemos tomar cuidado com a limitação gerada pela função.
Note que a coordenada vai de à , e portanto, temos que em obtemos a seguinte reta
isolando em termos de , temos que , e também temos que para , obtemos que
temos a reta . Portanto, a nossa integral é então dada por
vamos resolver esta integral agora! Saca só!
Passo 5
A integral interior é simplesmente dada por
Obtendo então que
Então, nosso volume é tal que
podemos identificar a primitiva como
ou, avaliando os limites , temos que
Portanto, nosso volume é simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!