Seja o domínio representado na figura, onde é a parte da circunferência , é a parte da circunferência , é a parte da circunferência . Reescrever a integral dupla
na forma iterada:
1. vendo como domínio de tipo 1
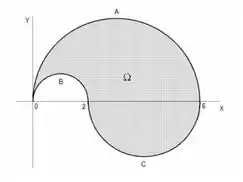
Passo 1
a) Pra nossa sorte, a questão está pedindo pra gente simplesmente escrever a integral como uma do tipo 1, e não resolvê-la. Então vamos lá. Precisamos lembrar que para escrever como do tipo 1, queremos o x variando entre constantes, enquanto o y varia entre funções, certo?
Bom, para isso então, vamos precisar separar em duas regiões:
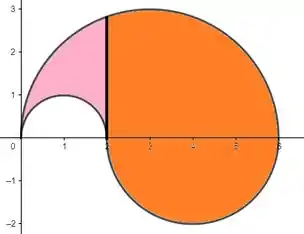
Passo 2
Temos à direita a região que eu falhei tristemente em destacar de laranja e a região à esquerda que eu também falhei ao tentar destacar de rosa. O que vale é a intenção, né? Continuemos....
Se você for observar, podemos escrever que x varia na região rosa de , e na região laranja de
Quanto a variação de y, observamos que na região rosa ela vai da circunferência B até A, e na região laranja vai de C até A.
Escrevendo a integral então ficamos:
Passo 3
Observa que separamos em duas integrais por termos separado em duas regiões.
Preciso também que você note quando usamos a parte superior e inferior da circunferência. Por exemplo, a curva ; queremos apenas a parte superior, então fazemos:
Como queremos só a parte de cima, ou seja, a positiva, ficamos então com
No caso da curva B, queremos a parte positiva, logo:
C queremos o lado negativo, logo:
Recapitulando, nossa integral descrita como uma do tipo 1 fica: