O valor da integral
Onde é o paralelogramo de vértices e é:
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O problema nos pede para calcularmos a área de um paralelogramo. Como sabemos que essa é a área? Porque temos que representa que é o elemento infinitesimal de área. Sendo assim, como é o nosso gráfico do paralelogramo?
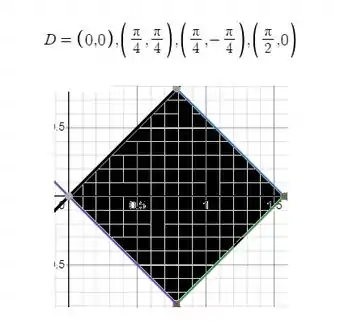
Então como que fazemos para achar a área desse paralelogramo? Temos que achar os limites de integração das variáveis e e enfim integrar na nossa função monstrinha que é . Então vamos lá?!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Podemos avaliar como é nossa região de integração. Já demos antes, lembra?
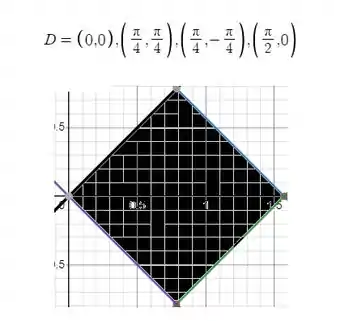
Como que podemos dividir essa área para ficar fácil para integração?! Podemos dividir em 4 partes e ver como que fica, saca só:
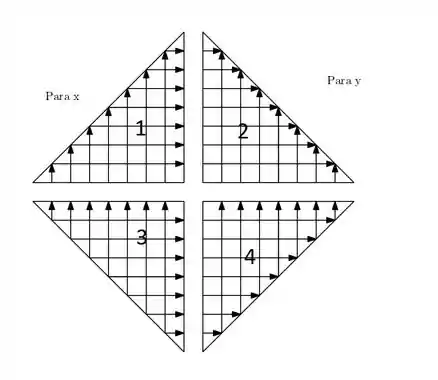
Veja como separamos! É uma maneira de separarmos o paralelogramo (ou mesmo qualquer outra figura, é bacana separarmos as nossas regiões de integração dessa maneira). “E Mogli, o que são essas setas?” Elas apontam a direção de integração que estamos operando, para cima para e para a direita para .
Então vamos observar as 4 partes e como ficam os limites de integração?
Passo 3
Uma maneira bacana para definirmos os limites de uma variável é pensarmos que os limites batem em uma parede, e ver qual que é essa parede que ele bate. Parece confuso, né?! Mas segue junto, porque vamos fazer isso muitas vezes nesse problema.
Para a primeira parte:
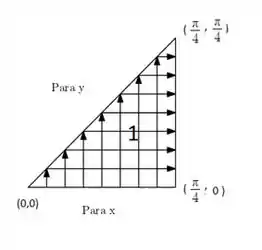
Vemos que e bate numa parede que é . Mas e ? Vemos que sai de e bate em uma reta. Que reta é essa? Bom, como podemos ver é uma reta que liga os pontos e . OK, sabendo disso podemos achar a equação da reta, certo?
Esta é uma técnica geral para acharmos a equação de uma reta que liga dois pontos. Isto é: colocamos os dois pontos e o ponto geral e , e sempre na última coluna colocamos , e assim encontrar o determinante. Saca só:
Então para acharmos a equação da reta basta aplicarmos a regra de Cramer. Logo:
Como saber se essa é mesmo a reta que liga esse pontos? Basta vermos no gráfico:
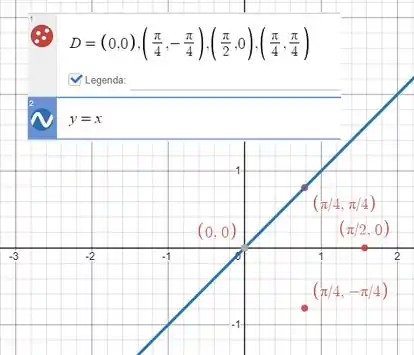
Sim! Ela é realmente a reta que liga os pontos e . Então como já sabíamos é uma técnica eficaz e vamos continuar usando nos próximos passos para acharmos as retas que ligam os pontos.
Voltando ao nosso raciocínio sai da parede e bate na parede .
Em resumo para a região 1:
Para a segunda parte:
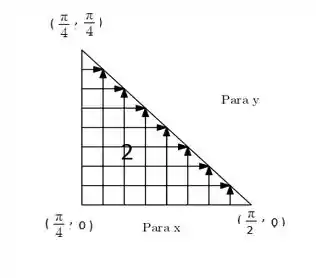
Vemos que sai da parede e anda até bater na parede . E para ? Bom, podemos ver que sai da parede e anda até uma parede. Que parede é essa? É a parede que é uma reta que liga os pontos e . Ok, pela mesma técnica que aplicamos anteriormente:
Então para acharmos a equação da reta basta aplicarmos a regar de Cramer. Logo:
Dividindo tudo por :
Então voltando ao raciocínio, temos que sai da parede e anda até a parede
Em resumo para a região 2:
Para a terceira parte:
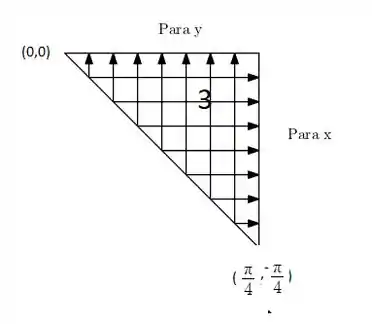
Vemos que e bate numa parede que é . Mas e ? sai de uma reta que liga os pontos e e bate na parede . Dissemos que ela sai de uma reta, que reta é essa? Bom sabendo que é uma reta que liga os pontos e , então a equação dela é:
Então para acharmos a equação da reta basta aplicarmos a regar de Cramer. Logo:
Então voltando ao raciocínio, temos que sai da parede e anda até a parede
Em resumo para a região 3:
Para a quarta e última parte:
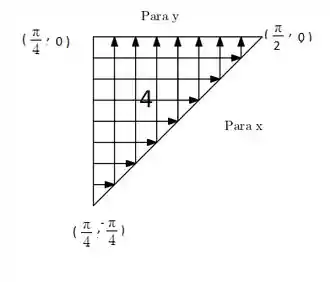
Vemos que sai da parede e anda até bater na parede . Mas novamente, e ? Vemos que sai de uma reta que liga os pontos e e percorre até bater na reta . Dissemos que ela sai de uma reta, que reta é essa? Bom sabendo que é uma reta que liga os pontos e então a equação dela é:
Então para acharmos a equação da reta basta aplicarmos a regar de Cramer. Logo:
Dividindo tudo por :
Então voltando ao raciocínio, temos que sai da parede e anda até a parede
Então resumindo para a região 4:
E agora que já temos todas as regiões, basta integrarmos.
Passo 4
Então temos a nossa integral de área nas 4 regiões:
Onde com , são as regiões que acabamos de definir. Qual ordem de integração devemos fazer, ou ? Claro que , certo? Porque tomamos todas as variáveis em função de . Aplicando os limites de integração, temos:
Eu sei o que pensa ao ver esse abacaxi:

Mas saca só que vamos usar uma malandragem no próximo passo.
Passo 5
Você não pensou que iríamos resolver essa integral, né?

Aqui uma declaração que devemos fazer: Embora tenhamos feito tudo até aqui, devemos lembrar que é uma prova que foi feita online, e, portanto, devemos realizar a prova nas mesmas circunstâncias que eles. E por que isso? Porque nesse momento chegamos em uma integral que só pode ser realizada por métodos computacionais numéricos, então vamos ver o que o computador nos dá?
Pelo desmos:
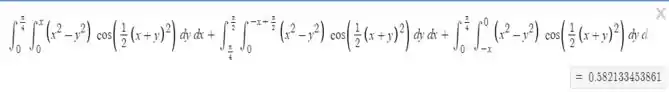
Só o Desmos foi capaz de calcular huehue. Mas então, o que garante que estamos certo? Vamos ver com qual alternativa o nosso resultado bate? Temos as respostas:
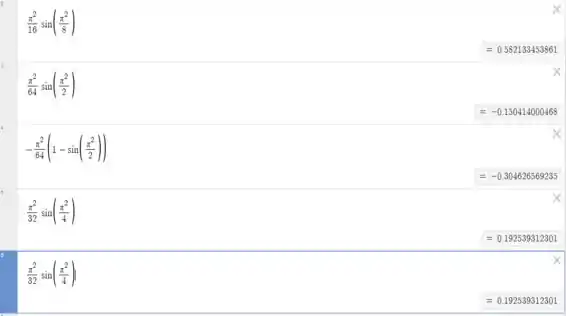
E vemos que o nosso resultado bate com , que é a alternativa a)
Então, a alternativa a) é a correta.
RAAAAAPAAAAZ, essa foi ossada não foi?! Mas você chegou até aqui junto comigo 😊. Muito obrigado e até a próxima!
Resposta
Alternativa a)