Calcule , onde é a região limitada pela reta e pela parábola .
Passo 1
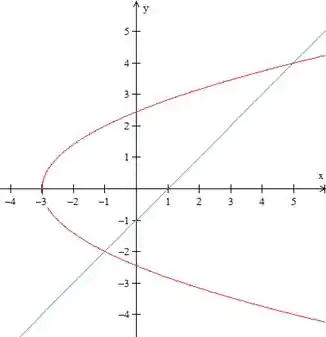
Vamos fazer um esboço para entender melhor a questão.
Observando a equação da parábola, vemos que o termo elevado ao quadrado é o , não o , como costumamos ver. Isso quer dizer que essa parábola está “virada de lado”, com eixo de simetria paralelo ao .
Como o número que multiplica é positivo, ela está virada para a direita (onde é positivo)
Fazendo , vemos que a parábola possui raízes (corta o eixo ):
Agora precisamos analisar a reta. Como o número que multiplica o é positivo, ela está virada para a direita.
O que estamos fazendo é uma análise rápida das equações do domínio, você não deve se preocupar em fazer um gráfico perfeito! Isso é apenas para termos uma noção do formato da área na hora de escrevê-la.
Passo 2
Essa região pode ser escrita tanto como tipo I como II. Porém, no primeiro caso seria preciso dividi-la em duas, pois na esquerda ela está limitada em cima e embaixo pela parábola e na direita, pela parábola e pela reta. Já se escrevermos como tipo II, a questão fica mais simples, pois teremos apenas a parábola na esquerda e a reta na direita.
É importante que você faça essas análises, para evitar contas desnecessárias!
Escrevendo como tipo II, então, precisamos colocar as equações da reta e da parábola em função de , isolando o :
Assim, teremos:
Para encontrar o intervalo de , temos que fazer a interseção entre as duas funções, igualando uma à outra.
Resolvendo
Portanto, temos e nosso domínio será:
Passo 3
Vamos substituir esses valores na integral
Passo 4
Agora vamos integrar em relação a :
Passo 5
Vamos integrar, então, em relação a :