UFSC, Joinvile, Cálculo II, Provas Profº Rómulo Castillo - P2 2016.2, Questão 4
Calcule onde R é a região delimitada por . Desenhe a região R de integração.
Passo 1
Eaew, belezinha?
A questão pede para a gente calcular a integral dada sobre uma região delimitada por duas retas com inclinações diferentes e pelo arco de circunferência de raio 2, dado pela equação Primeiro, vamos dar uma olhada na região R do plano xy, onde as curvas , estão representadas, respectivamente, pelas curvas azul, verde e vermelha:
Da imagem, a gente vê que as coordenadas x e y não são as mais apropriadas para resolver a integral sobre essa região. Ao invés disso, coordenadas polares parecem muito mais apropriadas, já que queremos integrar a função sobre uma seção circular! Então, vamos fazer as seguintes transformações: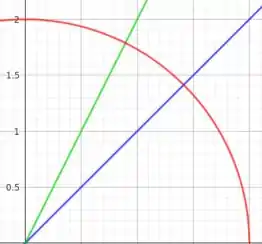
Fazendo essa transformação, temos que os nossos limites de integração para as coordenadas r e agora são
Onde os limites de se devem as retas com ângulos cujas tangentes são iguais à 1 e 2, respectivamente. Como , temos que o limite inferior é simplesmente 45 graus. Agora que já escrevemos nossa região R em novas coordenadas, precisamos ver como o integrando se transforma. Então vamos lá!
Passo 2
Quando fazemos uma transformação de coordenadas cartesianas para coordenadas polares, temos que o elemento de área dA = dxdy não é simplesmente o produto dos diferenciais dr d nas novas coordenadas. Precisamos multiplicá-lo pelo determinante Jacobiano da transformação:
Então, em uma transformação dessa, temos que a integral de uma função f(x,y) se escreve na forma
Onde r é o determinante Jacobiano da transformação de coordenadas. Então, podemos escrever a nossa integral como
Resolvendo essa integral, obtemos