Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 291234567891011121314151617181920212223242526272830313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Integral dupla sobre regiões gerais

Seja

R = x , y ∈ R 2 0 ≤ x ≤ y ≤ 1

  1. Seja F x , y uma função contínua definida na região R . Escreva a integral dupla

    2. I = ∬ R F x , y d x d y

    Obrigatoriamente na forma de uma integral iterada, integrando primeiro com respeito a x e em seguida com respeito a y .

  2. Escreva a integral dupla do item a obrigatoriamente como uma integral iterada, integrando primeiro com respeito a y e em seguida com respeito a x .

    3. Obs.: Obviamente, nos itens a e b não é pedido cálculo de integral.

  3. Calcule

I = ∬ R e y 2 d x d y

Passo 1

a )

Integrando primeiro em relação a x e depois em relação a y devemos ter, obrigatoriamente, uma região do tipo II, que vai ter essa cara aqui:

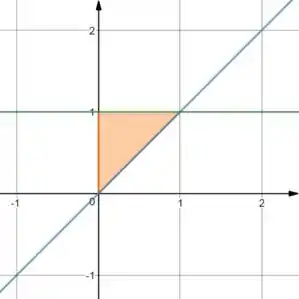
Isso quer dizer que, precisamos achar o intervalo de valores que o y varia, e depois o intervalo de funções que o x varia.

Pela descrição da região R e pela imagem vamos ter, para y

0 ≤ y ≤ 1

E para x

0 ≤ x ≤ y

A integral vai ficar

I = ∫ 0 1 ∫ 0 y F x , y d x d y

Passo 2

b )

Integrando primeiro em relação a y e depois em relação a x devemos ter, obrigatoriamente, uma região do tipo II.

Isso que dizer que, precisamos achar o intervalo de valores que o x varia, e depois o intervalo de funções que o y varia.

Pela descrição da região R vamos ter, para x

0 ≤ x ≤ 1

E para y

x ≤ y ≤ 1

A integral vai ficar

I = ∫ 0 1 ∫ x 1 F x , y d y d x

Passo 3

c )

Como a função e y 2 é muito difícil de integrar, vamos começar fazendo a integral em relação a x , ou seja, resolvendo a integral do item a

I = ∫ 0 1 ∫ 0 y e y 2 d x d y = ∫ 0 1 y - 0 e y 2 d y = ∫ 0 1 y e y 2 d y

Primeiro vamos ignorar os limites de integração e resolver a integral

∫ y e y 2 d y

Vamos resolver essa integral agora fazendo uma substituição simples,

u = y 2

Derivando

d u = 2 y d y

d u 2 = y d y

Substituindo na integral

∫ y e y 2 d y = ∫ e u d u 2 = 1 2 ∫ e u d u = 1 2 e u

Desubstituindo

1 2 e u = 1 2 e y 2

Passo 4

A integral vai ficar

∫ 0 1 y e y 2 d y = 1 2 e y 2 y = 0 1 = 1 2 e 1 2 - 1 2 e 0 2 = e 2 - 1 2 = e - 1 2

Resposta

  1. I = ∫ 0 1 ∫ 0 y F x , y d x d y
  2. I = ∫ 0 1 ∫ x 1 F x , y d y d x
  3. e - 1 2

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x