Calcule a integral iterada
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando essa integral iterada
A primeira coisa que você pensa é sair integrando, seguindo a ordem de integração: primeiro em depois em . Mas voc�� sabe integrar aquele que está dentro de uma raiz de índice ? Eu não saberia.... e agora, o que fazer? Nossa pergunta de milhões precisa de uma resposta de milhões...
Fazendo um desenho da região! Pegando os limites de integração vemos que
E esboçando essa região, temos isso aqui
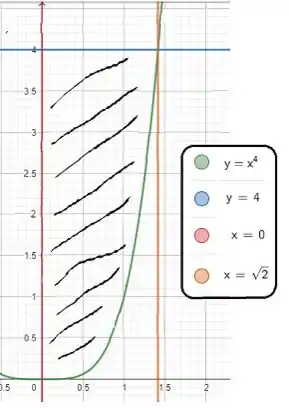

Invertendo a ordem temos o seguinte
Daí nossa integração começa em !
Mas relaxa, vou fazer passo a passo com você!
Passo 2
A integral que precisamos resolver é essa
Já sabemos que precisamos inverter os limites de integração, então nossa integral fica assim:
Resolvendo primeiro em e aplicando os limites temos
 Beleza?
Beleza?
Agora nossa missão é resolver essa integral em !
Passo 3
Nossa integral é essa aqui
De forma indefinida fica assim
Temos dentro da raiz, e um do lado de fora: isso significa que podemos usar a técnica de integração por substituição simples!
Assim temos
Agora é só aplicar os limites de integração!
Quando , quando , aí temos
Beleza? Espero ter ajudado!
Até a próxima!