UNICAMP – Cálculo 1 – Lista 3 – Limite e Continuidade
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
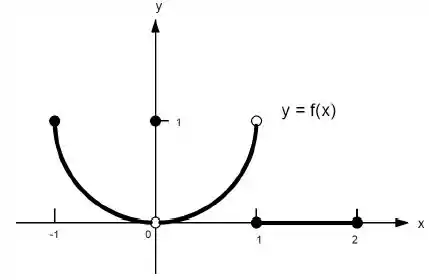
h)
Passo 1
Falaaa... beleza??
Nessa questão vamos analisar a afirmação “” e responder se ela é verdadeira ou falsa, com base no gráfico.
Pra isso vamos lembrar que quando temos um limite escrito da forma queremos saber o limite da função para valores que se aproximam de pela esquerda. De forma análoga, representa o limite para valores que se aproximam de pela direita.
Também vamos lembrar que para um limite existe, os limites laterais devem ser iguais.
Passo 2
A afirmação diz que o limite de quando está se aproximando de 1 é igual a . Pra isso ser verdade, os limites laterais devem ser iguais a zero. E, com isso, .
Repara no gráfico:
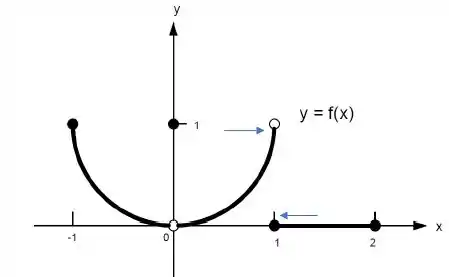
Quando está se aproximando de pela direita, o limite vale e quando está se aproximando de 1 pela esquerda, o limite 1. Portanto, o limite de quando se aproxima de não existe.
Falsa
Resposta
Falsa