6) Sem utilizar a regra de L’Hôpital, calcule os limites abaixo ou justifique caso os mesmos não existam:
b)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nosso objetivo aqui é calcular o limite de uma função que vamos chamar de , mas temos um porém! Não podemos usar a regra de L’Hôpital para calcular esses limites.
Evidenciando , temos
Então na verdade, vamos descobrir qual valor a função tende a assumir quando tende ao infinito.
Mas então como podemos fazer isso? 🤔🤔
Não podemos fazer o denominador ir para nem para quando aplicarmos o limite.
Então vamos começar dividindo em cima e em baixo por , que é o maior grau do denominador.
Entendeu? Bora ver como é na prática! 😎
Passo 2
Essa mudança não gera alteração na função pois estamos aplicando no numerador e no denominador.
Simplificando...
Aplicando o limite em , vamos obter
Uma das propriedades dos limites diz que , ou seja
Entendeu essa parte? 😎
Passo 3
Calculando o limite de para , sabemos que o limite de uma doma é igual a soma dos limites...
No limite de , vamos substituir e por consequência, . Já deve tender a pois
Ou seja...
Esse limite é muito especial pois para resolver ele, vamos dar uma olhada no círculo trigonométrico de raio .
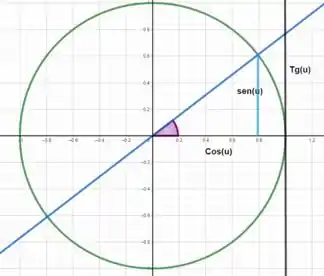
Vamos fazer algumas relações entre algumas áreas dessa figura...
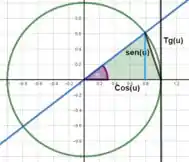
Dentro do mesmo círculo, tiramos três áreas para usar como análise.
Qual é a área verde? Essa área é um triangulo e como qualquer triangulo, sua área é o comprimento da base multiplicado pela altura dividido por , ou seja
E a área laranja? Essa é a área de um setor circular que é calculado como o ângulo dividido por multiplicado pela área do circulo
Já a área vermelha segue o que falamos sobre a área verde...
Entendeu como chegamos nessas áreas? 👀
Passo 4
Agora perceba que a área verde é menor que a área laranja que por sua vez é menor que a área vermelha, ou seja
Multiplicando tudo por e substituindo por , temos
Agora dividimos tudo por
Nesse momento vamos inverter as frações, mas pra isso, temos que inverter também os sinais de inequação
Perceba que se por negativo, também será no intervalo de a (contém nosso ponto de interesse).
Então não faz sentido deixar em modulo, logo
Substituindo por em , temos
Logo, pelo teorema do confronto, vemos que o limite de é igual a quando tende a
Portanto
Essa conta foi uma viajem, não é?
Mas relaxa, o pior já passou!
Passo 5
Continuando o cálculo dos limites...
O limite de entra na propriedade do limite de uma constante, ou seja, resulta na própria constante.
Já o limite de é obtido também pelo teorema do confronto, mas também podemos ver que como é limitado entre e cresce até o infinito, uma fração com um numerador bem pequeno e um denominador muito grande resulta em um número muito pequeno, quase , então...
Calculando o limite do denominador
Vamos separar pela soma dos limites
O limite de se encaixa no limite de uma constante, ou seja
Já os limites de e se encaixam na ideia do limite de , ou seja, numerador pequeno e denominador muito grande...
Tranquilo até aqui? 👍
Passo 6
Substituindo os resultados dos limites na fração dos limites, temos
Como
Então chegamos à conclusão de que
O limite que queremos é igual a , ou seja, a função tende a esse valor quando tende ao infinito!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
