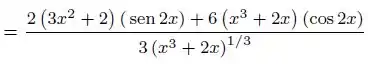Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regra da Cadeia

Ver Teoria
Exercício 236123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Regras de Derivação

Derive a função (se possível, simplifique antes e/ou depois de derivar).

f x = s e n 2 x . x 3 + 2 x 2 3

Passo 1

Para derivar essa função, vamos usar a regra do produto. Relembrando...

f x g x ' = f ' x g x + f ( x ) g ' ( x )

Então

f ' x = s e n 2 x ' ∙ x 3 + 2 x 2 3 + s e n 2 x ∙ x 3 + 2 x 2 3 '

Passo 2

Agora vamos derivar isso tudo aos poucos.

Começando por s e n 2 x ' .

Usando a regra da cadeia;

s e n 2 x ' = cos ⁡ 2 x ∙ 2

s e n 2 x ' = 2 cos ⁡ 2 x

Passo 3

Agora vamos derivar x 3 + 2 x 2 3 ' .

Novamente, usando a regra da cadeia:

x 3 + 2 x 2 3 ' = 2 3 x 3 + 2 x - 1 3 ∙ 3 x 2 + 2

x 3 + 2 x 2 3 ' = 2 3 x 2 + 2 3 x 3 + 2 x 1 3

Passo 4

Juntando tudo:

f ' x = 2 cos ⁡ 2 x ∙ x 3 + 2 x 2 3 + s e n 2 x ∙ 2 3 x 2 + 2 3 x 3 + 2 x 1 3

Fazendo o mmc:

f ' x = 2 cos ⁡ 2 x ∙ x 3 + 2 x 2 3 ∙ 3 x 3 + 2 x 1 3 + s e n 2 x ∙ 2 3 x 2 + 2 3 x 3 + 2 x 1 3

Organizando:

f ' x = 6 cos ⁡ 2 x x 3 + 2 x 1 + 2 3 x 2 + 2 s e n 2 x 3 x 3 + 2 x 1 3

Resposta

Exercícios de Livros Relacionados

Encontre a derivada da função.y = ((x^2 + 1)/(x^2 - 1))^3
Encontre a derivada da função.(d)/(d x) 2^(sen ( pi x ))
Encontre a derivada da função. y = r r 2 + 1
Encontre a derivada da função. G y = y - 1 4 y 2 + 2 y 5
Encontre a primeira e a segunda derivadas da função. y = e α x β x