Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 116123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere o campo vetorial F → : R 3 → R 3 dado por

F → x ,   y ,   z = y z + 1 3 y 3 ,   x y 2 - x z ,   z 2 + sin ⁡ e z .

  1. Determine o rotacional de F → .
  2. Calcule ∫ C   F → ∙ d r → ao longo da curva C dada pela interseção da superfície z = x y com a superfície cilíndrica x 2 + y 2 = 9 , com orientação no sentido anti-horário quando vista de cima.

Passo 1

Letra a) bem... Aqui não tem segredo, basta aplicar a fórmula de rotacional, se lembra?

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Onde o campo vetorial F x ,   y ,   z = y z + 1 3 y 3 ,   x y 2 - x z ,   z 2 + sin ⁡ e z , sendo cada uma dessas entradas F x , y   z = F 1 ,   F 2 ,   F 3 . Basta aplicar essas derivadas e correr para o abraço!:D

1 º                                                                 ∂ F 3 ∂ y = ∂ z 2 + sin ⁡ e z ∂ y = 0

2 º                                                                       ∂ F 2 ∂ z = ∂ x y 2 - x z ∂ z = - x

3 º                                                                           ∂ F 1 ∂ z = ∂ y z + 1 3 y 3 ∂ z = y

4 º                                                                 ∂ F 3 ∂ x = ∂ z 2 + sin ⁡ e z ∂ x = 0

5 º                                                         ∂ F 2 ∂ x = ∂ x y 2 - x z ∂ x = y 2 - z

E por fim, podemos calcular a última derivada

6 º                                                   ∂ F 1 ∂ y = ∂ y z + 1 3 y 3 ∂ y = z + y 2

Jogando todos esses resultados no vetor rotacional:

r o t   F → = 0 - - x ,   y - 0 ,   y 2 - z - z + y 2

r o t   F → = x ,   y ,   - 2 z

Passo 2

Letra b) como você já pode notar, o rotacional simplifica muuuuito a nossa vida. Como o problema quer que calculemos a integral de linha em C , vamos tentar utilizar S t o k e s !

∫ C   F → ∙ d r → = ∬ S   r o t   F → ∙ n → d S

Ok! Sabemos que vamos utilizar Stokes aqui, mas quem é essa superfície S aí mesmo? Aliás, quem é a curva C ?!

Passo 3

Infelizmente, aqui, a gente não pode contar com o desenho da curva para nos ajudar, pois ela não é uma curva simples :(

Porém... (EBA! Têm um porém! :D) a gente não precisa de desenhar a curva pois a gente vai matar por Stokes, e para isso, basta a gente conhecer uma superfície delimitada por C !

Agora, vamos pensar juntos, que superfície pode ser essa?

Como a curva está em cima do gráfico da equação z = x y , essa superfície é uma boa, não acha?

Mas apenas queremos o pedacinho dessa superfície que está dentro da curva C , e olha que legal: a curva C está em cima do cilindro x 2 + y 2 = 9 , logo a superfície vai estar dentro desse cilindro.

Resumindo... vamos utilizar a superfície no interior do cilindro em cima do gráfico de z = x y , entendeu? :D

Passo 4

Bem, mas chega de falar e bora pras contas!

Não podemos continuar sem uma parametrização para a superfície, e aí vai uma:

Como estamos trabalhando com um gráfico de uma função ( z = x y ), podemos pensar em uma parametrização explícita:

φ x ,   y = x ,   y ,   z ( x ,   y )

Ou seja

φ x ,   y = x ,   y ,   x y

Como já dissemos, essa superfície está dentro do cilindro de equação x 2 + y 2 = 3 2

Logo, os parâmetros x e y só podem variar dentro dessa equação de um círculo, ou seja:

x 2 + y 2 ≤ 3 2

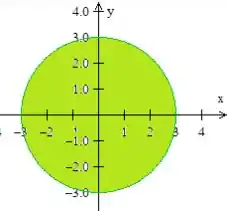
A gente pode chamar essa região de D , só para facilitar

Passo 5

Em todo problema com superfície, sim a gente precisa de encontrar vetor  N → norma a ela.

O que aqui não é um grande problema, já que parametrizamos em gráfico de função z = x y , logo podemos utilizar o bizuzão

N → x ,   y = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1

Calculando...

N → x ,   y = - y ,   - x ,   1

Agora aqui envolve muita atenção! Qual vetor normal pegamos: esse ou o inverso desse?

Bem, o problema disse que se a gente olhasse para a superfície de cima para baixo, veríamos a borda girando no sentido anti-horário:

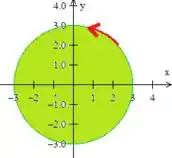
Logo, pela regra da mão direita, imaginado o eixo z saindo da tela (pois estamos visualizando de cima para baixo), nota-se que queremos o vetor normal com z positivo, logo queremos justamente esse vetor normal aí, percebeu?

Passo 6

Podemos depois de tudo isso retornar para Stokes, bora?

∫ C   F → ∙ d r → = ∬ S   r o t   F → ∙ n → d S

Substituindo esses caras que já calculamos na integral de superfície apenas tomando o cuidado de que n →   d S = N →   d x d y

∬ S   r o t   F → ∙ n → d S = ∬ D   x ,   y ,   - 2 z ∙ N →   d x d y

Substituindo N → que acabamos de encontrar

∬ D   x ,   y ,   - 2 z ∙ - y ,   - x ,   1   d x d y

Calculando esse produto interno aí

∬ D   - x y - x y - 2 z   d x d y =

∬ D   - 2 x y - 2 z   d x d y

Bem, não podemos ter z lá dentro, então substituímos z pela parametrização z = x y

∬ D   - 2 x y - 2 x y   d x d y =

∬ D   - 4 x y   d x d y

Bem, agora não tem mais nada de integral de superfície, basta calcular essa integral dupla e correr para o abraço!

Passo 7

Como a região D de integração é um círculo, para resolver essa integral dupla, vamos fazer ua substituição por coordenadas polares

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

Agora quais são os limites desses novos caras?

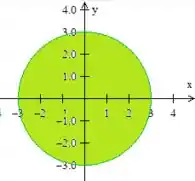
Bem, r varia de 0 até o raio máximo da região

0 ≤ r ≤ 3

E theta, bem ele varia...

0 ≤ θ ≤ 2 π

Substituindo na integral dupla....

∬ D   - 4 x y   d x d y = - 4 ∫ 0 2 π ∫ 0 3 r cos ⁡ θ ∙ r sin ⁡ θ ∙ J d r d θ

- 4 ∫ 0 2 π ∫ 0 3 cos ⁡ θ ∙ sin ⁡ θ ∙ r 3 d r d θ

Como essa é uma integral definida em uma região retangular, podemos...

- 4 ∫ 0 2 π ∫ 0 3 cos ⁡ θ ∙ sin ⁡ θ ∙ r 3 d r d θ = - 4 ∫ 0 2 π cos ⁡ θ ∙ sin ⁡ θ d θ ∙ ∫ 0 3 r 3 d r

Passo 8

Resolvendo primeiro

∫ 0 2 π cos ⁡ θ ∙ sin ⁡ θ d θ =

Fazendo uma substituição sin ⁡ θ = a

d a = cos ⁡ θ d θ

Não se esquecendo dos limites de a

θ = 0         ⇒                 a = sin ⁡ 0 = 0

θ = 2 π       ⇒             a = sin ⁡ 2 π = 0

OPA! Limites iguais? Então essa integral da zero:

∫ 0 2 π cos ⁡ θ ∙ sin ⁡ θ d θ = ∫ 0 0 a d a = 0

Se essa integral zerou, então o produto é

- 4 ∫ 0 2 π cos ⁡ θ ∙ sin ⁡ θ d θ ∙ ∫ 0 3 r 3 d r = 0

Logo, pelo teorema de Stokes

∫ C   F → ∙ d r → = ∬ S   r o t   F → ∙ n → d S = 0

Resposta

Letra a) r o t   F → = x ,   y ,   - 2 z

Letra b)

∫ C   F → ∙ d r → = 0

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê