Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 2:

Seja S a superfície (regular por partes) constituída pela união dos três triângulos contidos nos planos coordenados e de vértices 0 ,   0 ,   0 , 1 ,   0 ,   0 , 0 ,   1 ,   0 , 0 ,   0 ,   1 . O bordo de S é uma curva (regular por partes) fechada que consideraremos orientada de modo que sua projeção no plano x y é percorrida no sentido anti-horário. Calcule o trabalho realizado pelo campo de forças espacial

F = cos ⁡ x + x z , e y + x y , z y + z 3 ,     x ,   y ,   z ∈ R 3

sobre uma partícula cuja trajetória é ∂ S .

Passo 1

Então, uma coisa que precisamos já ter em mente imediatamente após ler o enunciado, é sobre o que iremos fazer para matar o problema. Trabalho de um campo, a essa altura dos nossos estudos, é dado por uma integral de linha em cima da curva da trajetória, no caso ∂ S :

∫ ∂ S   F → ⋅ d r →

Como o campo F não é nada muito elegante, e a curva também parece um pouco chata, não resolveremos essa integral de linha direto e sim tentar aplicar o teorema de Stokes.

Para ter certeza se é de fato Stokes, vem comigo calcular o rotacional ;)

Passo 2

O rotacional é dado por...

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Como...

F = cos ⁡ x + x z ⏟ F 1 , e y + x y ⏟ F 2 , z y + z 3 ⏟ F 3

Calculando as derivadas parciais...

r o t   F → = z - 0 ,   x - 0 ,   y - 0

r o t   F → = z ,   x ,   y

Com um rotacional simples desse, está provado que vamos utilizar o teorema de Stokes:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Agora, não podemos sair aplicando essa igualdade assim... Sem avaliar as condições do Teorema, então vamos lá!

Passo 3

O teorema nos exige basicamente três coisas:

1º - Uma superfície S que delimita a curva borda ∂ S .

2º - Uma superfície orientada positivamente em relação a borda.

3º - Um campo F sem singularidades.

Passo 4

A primeira exigência nos pede então uma curva ∂ S que seja borda de S . Mas quem é a curva que o problema quer mesmo? Será que ela é uma curva fechada? Bem para responder essas indagações, desenhamos a curva:

Primeiro inserimos os quatro vértices dado no problema: 0 ,   0 ,   0 , 1 ,   0 ,   0 , 0 ,   1 ,   0 , 0 ,   0 ,   1

Como os triângulos estão nos planos coordenados... A superfície S é essa superfície composta aqui oh:

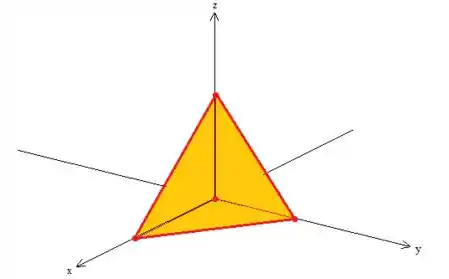
Repare que a borda dessa superfície é a curva que queremos... A chamada ∂ S

Passo 5

Quanto à segunda exigência do Teorema, sobre a superfície estar orientada positivamente em relação à borda, vejamos!

Pelo enunciado, a projeção da curva no plano x y gira no sentido anti-horário, assim, a curva só pode estar também girando no sentido...

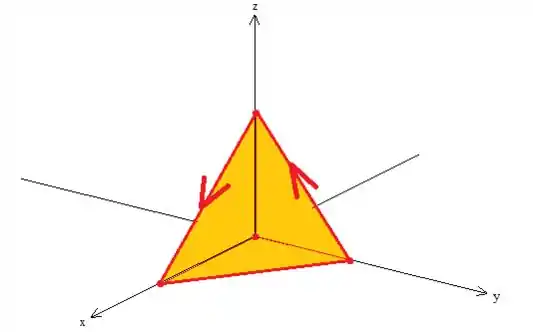
Pela regra da mão direita então, aonde os dedos vão ao sentido de giro da curva e o polegar aponta no sentido do vetor norma, o vetor normal deve estar apontando para dentro do primeiro octante...

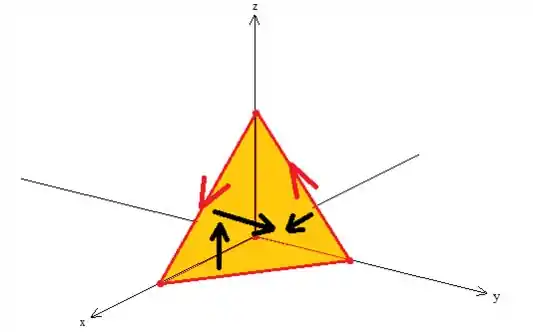
E prontinho! Superfícies e curva orientados positivamente ;)

Passo 6

A última exigência se trata do campo: o campo não pode ter singularidades onde estamos trabalhando

F = cos ⁡ x + x z , e y + x y , z y + z 3

Como não temos nenhum problema de definição em nenhum ponto, como uma divisão por zero ou algo assim, o campo está ok.

Passo 7

Nas condições do Teorema, podemos aplicar a igualdade de Stokes:

∫ ∂ S   F → ⋅ d r → = ∬ S   r o t F → ⋅ n →   d S

Aqui tem mais um detalhe muito importante: se você olhar para o esboço da superfície S novamente

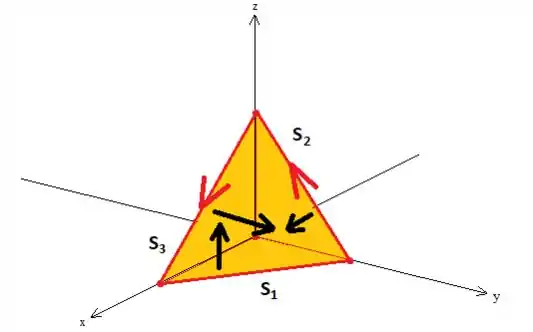
Vai perceber que a superfície S que delimita ∂ S , é uma superfície composta de outras três... S 1 , S 2 e S 3 ...

Então, temos que separar a integral de superfície em...

∫ ∂ S   F → ⋅ d r → = ∬ S 1   r o t F → ⋅ n →   d S + ∬ S 2   r o t F → ⋅ n →   d S + ∬ S 3   r o t F → ⋅ n →   d S

Se queremos a integral de linha, basta calcular essas três integrais de superfícies e matar o problema (embora pareça que estamos ficando maluco por fazer três integrais ao invés de uma de linha, ainda é o processo mais rápido, vai por mim ). Bora lá?

Passo 8

Vamos começar pela primeira integral de linha em S 1 ...

∬ S 1   r o t F → ⋅ n →   d S

  • Precisamos parametrizar essa superfície em um primeiro momento. Como é um plano que passa por z = 0 ...

    • σ x ,   y = x ,   y ,   0

    Para saber a variação de x y , olhemos para a superfície S 1 de cima para baixo:

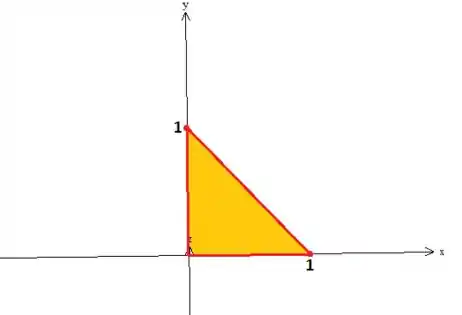
    Repare que podemos descrever essa região como do tipo 1 , ou seja, x varia de 0 a 1 enquanto o y varia de 0 até essa reta oblíqua

    0 ≤ y ≤ r e t a   o b l í q u a

    A reta oblíqua é a reta y + x = 1 , pois quando x = 1 , y = 0 e vice versa, sacou?

    0 ≤ y ≤ 1 - x

  • Calculemos agora o n → d S ...

    • n → d S = N →   d S

    Como a superfície foi parametrizada como gráfico de função, podemos encontrar o vetor norma fazendo...

    N → = - ∂ z ∂ x ,   - ∂ z ∂ y ,   1 = 0 ,   0 ,   1

  • Devemos substituir no campo rotacional que estamos calculando a integral de superfície a parametrização...

    • r o t   F → x ,   y ,   z = z ,   x ,   y

    r o t   F → σ x ,   y = 0 ,   x ,   y

    Agora é só voltar para a integral de superfície...

    ∬ S 1   r o t F → ⋅ n →   d S = ∫ 0 1 ∫ 0 1 - x 0 ,   x ,   y ⋅ 0 ,   0 ,   1   d y d x =

    ∫ 0 1 ∫ 0 1 - x y   d y d x

    Calculando a integral dupla...

    ∫ 0 1 ∫ 0 1 - x y   d y d x = ∫ 0 1 ∫ 0 1 - x y   d y d x =

    ∫ 0 1 y 2 2 0 1 - x d x = ∫ 0 1 1 - x 2 2 d x =

    1 2 ∫ 0 1 1 - 2 x + x 2   d x = 1 2 x - x 2 + x 3 3 0 1 =

    1 2 1 - 1 + 1 3 = 1 6

    Passo 9

    Fazendo o mesmo para a outra integral de superfície...

    ∬ S 2   r o t F → ⋅ n →   d S

  • Parametrizando S 2 ...

    • σ 2 y ,   z = 0 ,   y ,   z

    Onde os limites são bem semelhantes já que a reta obliqua dessa vez é y + z = 1 ...

    0 ≤ y ≤ 1

    0 ≤ z ≤ 1 - y

  • Calculando o n →   d S ...

    • n →   d S = N →   d y d z

    Como parametrizamos como gráfico de função... x y ,   z = 0 ...

    N → = 1 ,   - ∂ x ∂ y , - ∂ x ∂ z   = 1 ,   0 ,   0

  • A função...

    • r o t   F → x ,   y ,   z = z ,   x ,   y

    r o t   F → σ 2 y ,   z = z ,   0 ,   y

    Substituindo...

    ∬ S 2   r o t F → ⋅ n →   d S = ∫ 0 1 ∫ 0 1 - y z ,   0 ,   y ⋅ 1 ,   0 ,   0   d z d y

    ∫ 0 1 ∫ 0 1 - y z   d z d y

    Já calculamos essa mesma integral no passo anterior, só que as variáveis tinham outro nome. Como nomenclatura não interfere no resultado...

    ∫ 0 1 ∫ 0 1 - y z   d z d y = 1 6

    Passo 10

    Por último e não morra de tédio, calculemos a integral me cima de S 3 ...

    ∬ S 3   r o t F → ⋅ n →   d S

  • A parametrização...

    • σ 3 x ,   z = x ,   0 ,   z

    Onde novamente...

    0 ≤ x ≤ 1

    0 ≤ z ≤ 1 - x

    Perceba que dá muito semelhante às outras, pois todas são triângulos...

  • n →   d S ... Como y x ,   z = 0 ...

    • n →   d S = N →   d x d z

    N → = - ∂ y ∂ x ,   1 ,   - ∂ y ∂ z = 0 ,   1 ,   0

  • Trocando a função...

r o t   F → x ,   y ,   z = z ,   x ,   y

r o t   F → σ 3 x ,   z = z ,   x ,   0

∬ S 3   r o t F → ⋅ n →   d S = ∫ 0 1 ∫ 0 1 - x z ,   x ,   0 ⋅ 0 ,   1 ,   0   d z d x

∫ 0 1 ∫ 0 1 - x x   d z d x

Epa! essa integral aí não é igual as outras...

∫ 0 1 ∫ 0 1 - x x   d z d x = ∫ 0 1 x ∫ 0 1 - x   d z d x =

∫ 0 1 x 1 - x d x = ∫ 0 1 x - x 2 d x =

x 2 2 - x 3 3 0 1 = 1 2 - 1 3 = 1 6

Passo 9

Voltando para a integral que queremos, a de linha...

∫ ∂ S   F → ⋅ d r → = ∬ S 1   r o t F → ⋅ n →   d S + ∬ S 2   r o t F → ⋅ n →   d S + ∬ S 3   r o t F → ⋅ n →   d S

∫ ∂ S   F → ⋅ d r → = 1 6 + 1 6 + 1 6 =

1 2

Resposta

1 2

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê