Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 126123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFRJ, Sem Campus, Cálculo 3, Provas Antigas, P2, 2022.2, 2

Seja S o pedaço do cone z = x 2 + y 2 acima do plano z = 0 e embaixo do plano z = 1 . Calcule I = ∬ S ( x 2 + y 2 ) d S .

Passo 1

Fala, galera! Vamos resolver essa questão!

O enunciado pediu pra gente calcular a integral de I = ∬ S ( x 2 + y 2 ) d S , onde S é a superfície do cone que está entre os planos z = 0 e z = 1 . Essa daqui, olha só:

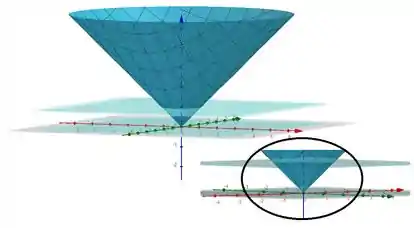
Repara que em z = 0 o cone se “fecha”, então a fronteira de S é apenas a interseção entre o cone e o plano z = 1 , que é uma circunferência de raio 1 . Então, nossa região de integração D é dada por:

D = R 2     x 2 + y 2 ≤ 1 }

A partir daí, o que nós vamos fazer pra calcular a integral de superfície de I é escrever ela dessa forma:

∬ S f ( x ,   y ,   z ) d S = ∬ D f ( x ,   y ,   g x ,   y ) ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1   d D

Em que f x ,   y ,   z = x 2 + y 2 , g x ,   y = z e d S = ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1 . Então, nós precisamos encontrar as derivadas parciais ∂ z ∂ x e ∂ z ∂ y , colocar na raiz de d S e substituir na integral junto com a função f .

Vamos lá!

Passo 2

Vamos começar calculando a derivada parcial de z = x 2 + y 2 em relação a x , usando a Regra da Cadeia (derivada da função de fora aplicada na função de dentro, vezes a derivada da função de dentro):

∂ z ∂ x = 1 2 x 2 + y 2 ∂ ∂ x ( x 2 + y 2 )

∂ z ∂ x = 2 x 2 x 2 + y 2 = x x 2 + y 2

Calculando agora a derivada parcial de z em relação a y , temos:

∂ z ∂ y = 1 2 x 2 + y 2 ∂ ∂ y ( x 2 + y 2 )

∂ z ∂ y = 2 y 2 x 2 + y 2 = y x 2 + y 2

Substituindo na equação de d S :

d S = ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1   d D

d S = x x 2 + y 2 2 + y x 2 + y 2 2 + 1     d D

Elevando os termos ao quadrado:

d S = x 2 x 2 + y 2 + y 2 x 2 + y 2 + 1     d D

Tirando o M . M . C dentro da raiz:

d S = x 2 + y 2 x 2 + y 2 + 1     d D

Simplificando a fração:

d S = 1 + 1   d D

d S = 2     d D

Passo 3

Agora podemos montar nossa integral:

∬ S f ( x ,   y ,   z ) d S = ∬ D f ( x ,   y ,   g x ,   y ) ∂ z ∂ x 2 + ∂ z ∂ y 2 + 1   d D

Com f x ,   y ,   z = x 2 + y 2 e d S = 2     d D , temos:

∬ D x 2 + y 2 ∙ 2   d D

Colocando a constante pra fora da integral:

2 ∬ D ( x 2 + y 2 )   d D

Como vimos no passo 1 , nossa região de interseção na superfície é uma circunferência, então, pra facilitar nossa vida, podemos transformar a integral para coordenadas polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

Daí, nós temos x 2 + y 2 = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ = r 2 (pela identidade trigonométrica cos 2 ⁡ θ + sin 2 ⁡ θ = 1 ). Além disso, o ângulo θ varia de 0 a 2 π na circunferência, e o raio, como nós vimos no passo 1 , varia de 0 a 1 . Ou seja:

0 ≤ θ ≤ 2 π

0 ≤ r ≤ 1

Então, nossa integral fica:

2 ∬ D ( x 2 + y 2 )   d D = 2 ∫ 0 2 π ∫ 0 1 r 2   r d r d θ

= 2 ∫ 0 2 π ∫ 0 1 r 3   d r d θ

Passo 4

Agora vamos calcular nossa integral. Integrando primeiro em relação a r , temos:

2 ∫ 0 2 π ∫ 0 1 r 3   d r d θ = 2 ∫ 0 2 π r 4 4 0 1 d θ

Aplicando os intervalos de integração:

2 ∫ 0 2 π ( 1 ) 4 4 - 0 4 4 d θ

2 ∫ 0 2 π 1 4 d θ

A gente pode colocar essa constante do lado de fora da integral também:

2 4 ∫ 0 2 π d θ

Integrando agora em relação a θ :

2 4 θ 0 2 π

Aplicando os intervalos de integração em θ :

2 4 2 π - 0

= 2 2 4 π = 2 2 π  

Então, nossa integral I = ∬ S ( x 2 + y 2 ) d S é igual a 2 2 π , mas você também pode escrever o resultado dessa forma:

I = π 2

Que é a mesma coisa (basta multiplicar 2 2 no resultado pra ver).

Valeu, galera! Até a próxima! 😉

Resposta

I = π 2

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê