Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 112123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Seja S ⊂ R 3 a superfície regular determinada pelas igualdades e desigualdades

x 2 + y 2 = 2 - z 2 ,                   x 2 + y 2 ≤ 1 ,                 z ≤ 0

e orientada pelo vetor normal unitário continuo cuja coordenada z é negativa, e seja F → o campo de classe C 1 :

F → x ,   y ,   z = z y e y x + y ,   z x e x y ,   e x y z

  1. Faça um esboço de S .
  2. Calcule o rotacional de F → .
  3. Calcule o fluxo do r o t   F → através de S . Dica: Aplique o teorema de Stokes para reemplazar (substituir) S por outra superfície orientada S - tal que ∂ S = ∂ S - .

Passo 1

  1. Então, primeiramente quem são essas três igualdades?

    2. Bem, a primeira delas se a gente passar aquele termo - z 2 pro outro lado, teremos

    x 2 + y 2 + z 2 = 2

    que nos representa uma esfera de um raio bem escroto: R = 2 ou se preferir 2 4 .

    A segunda, x 2 + y 2 ≤ 1 , também não é complicada! Se a gente elevar ao quadrado ambos termos dela, obteremos

    x 2 + y 2 ≤ 1

    Ou seja, essa inequação é um cilindro de raio 1 com o eixo em z , ele só veio de uma forma estranha mesmo!

    Bem, quanto a terceira inequação, z ≤ 0 , bem, ela apenas está indicando que quer apenas as partes abaixo do plano z = 0 mesmo.

    Se a gente colocar essas três coisas juntas no espaço, teremos

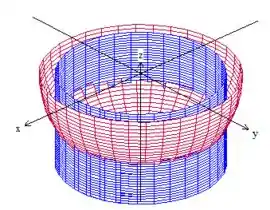
    Bem, a superfície S está em cima de esfera (devido à igualdade) mas a gente só quer a parte que está dentro do cilindro de raio 1 , ou seja, a superfície S é

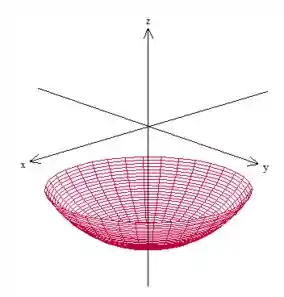
    Passo 2

  2. Bem aqui não tem mistério algum, neh? Basta aplicar a fórmula do rotacional e fechou!

    3. r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

    Onde o campo vetorial nesse caso é

    F → x ,   y ,   z = z y e y x + y ⏟ F 1 ,   z x e x y ⏟ F 2 ,   e x y z ⏟ F 3

    Basta agora calcular essas 6 derivadas parciais e prontinho!:)

    Passo 3

    Vem comigo:

    1 º                                                                       ∂ F 3 ∂ y = ∂ e x y z ∂ y

    Tendo cuidado na hora da regra da cadeia...

    ∂ F 3 ∂ y = e x y z ∙ x z

    Os outros seguem o modelo:

    2 º                                   ∂ F 2 ∂ z = ∂ z x e x y ∂ y = x e x y

    3 º                   ∂ F 1 ∂ z = ∂ z y e y x + y ∂ z = y e y x

    4 º                           ∂ F 3 ∂ x = ∂ e x y z ∂ x = e x y z ∙ y z

    5 º                                                                 ∂ F 2 ∂ x = ∂ z x e x y ∂ x

    Epa! Aqui apareceu algo diferente! Teremos que além da regra da cadeia, aplicar a regra do produto, okay?

    ∂ F 2 ∂ x = z ( e x y + x e x y ∙ y )

    Por fim,

    6 º                                     ∂ F 1 ∂ y = ∂ z y e y x + y ∂ y

    Além de ser parecido com o 5 º esse ainda tem uma soma. Então atenção!

    ∂ F 1 ∂ y = z ( e y x + y e y x ∙ x ) + 1

    Passo 4

    Voltando com tudo pro rotacional teremos...

    r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

    r o t   F → = x z e x y z - x e x y ,   y e y x - y z e x y z ,   z ( e x y + x e x y ∙ y ) - z ( e y x + y e y x ∙ x ) + 1

    Simplificando um pouquinho o terceiro membro, ficaremos

    r o t   F → = x z e x y z - x e x y ,   y e y x - y z e x y z ,   - 1

    Passo 5

  3. Queremos agora calcular a integral de superfície do rotacional e obviamente vamos usar a dica e chamar o nosso amigo S t o k e s !:)

Stokes nos fala que se a gente tem uma curva fechada no espaço ( ∂ S ), se o campo não tiver singularidades então

∮ ∂ S     F → d r → = ∬ S   r o t   F → ∙ n →   d S

Não se assuste porque essa integral de linha aí nem vai entrar na jogada!

Mas ué! Porque ela está ai então?

Porque pelo teorema de Stokes qualquer superfície que tiver como borda a curva fechada ∂ S tá valendo. A curva fechada no nosso caso é essa azulzinha aqui:

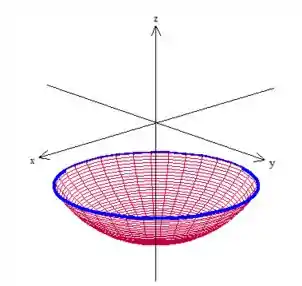
Essa curva é borda de outra superfície S - ainda mais easy pelo visto: um plano com z constante!

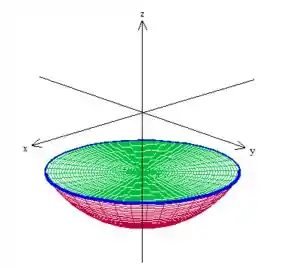
Logo, pelo teorema de Stokes...

∮ ∂ S -     F → d r → = ∬ S -   r o t   F → ∙ n →   d S

Lembrando que ∂ S = ∂ S - , pois tanto a superfície vermelha quanto a verde tem a mesma borda azul

∮ ∂ S -     F → d r → = ∮ ∂ S     F → d r → = ∬ S   r o t   F → ∙ n →   d S

então

∬ S   r o t   F → ∙ n →   d S = ∬ S -   r o t   F → ∙ n →   d S

Se a gente quer a integral em S basta encontrar o resultado na segunda integral que é bem mais fácil!

Passo 2

Bem, pra resolver aquela integral em S - , precisamos parametrizar a superfície em primeiro lugar.

Ué, mas qual é a equação desse plano?

Pow, a equação dele é a intersecção do cilindro com a esfera, ou seja

x 2 + y 2 = 1 x 2 + y 2 + z 2 = 2  

Substituindo e equação de cima na da esfera em baixo

1 + z 2 = 2

z 2 = 2 - 1

Extraindo a raiz lembrando que queremos a parte onde z é negativo

z = - 2 - 1

A parametrização ficará então, utilizando uma parametrização explícita,

σ x , y = x ,   y ,   - 2 - 1

Toda vez que calculamos uma parametrização, não podemos esquecer-nos dos limites dos nossos novos parâmetros, certo?

Os parâmetros x e y nesse caso varia dentro da circunferência delimitada pelo cilindro de raio 1 (chamaremos esta região de D ):

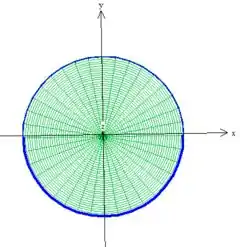
Passo 3

O vetor normal é, pelo bizu de vetor normal de uma parametrização explícita...

N → = - ∂ z ∂ x , - ∂ z ∂ y , 1

N → = 0 ,   0 ,   1

Agora um detalhe muito importante! Qual vetor normal queremos? Esse ou o inverso desse?

Bem, se lembrarmos do enunciado, ele quer que o vetor normal tenha coordenada z negativa, logo queremos o vetor normal oposto a esse, ou seja:

N → = 0 ,   0 , -   1

Passo 4

Voltando agora para a integral de superfície que temos que resolver

∬ S -   r o t   F → ∙ n →   d S

Pelo teoria temos

∬ S -   r o t   F → ∙ n →   d S = ∬ D   r o t   F → ∙ N →   d x d y

Substituindo essas coisas que já determinamos

∬ S -   r o t   F → ∙ n →   d S = ∬ D   x z e x y z - x e x y ,   y e y x - y z e x y z ,   - 1 ∙ 0 ,   0 , -   1   d x d y

Efetuando esse produto interno de vetores

∬ S -   r o t   F → ∙ n →   d S = ∬ D   1 d x d y

O que essa integral dupla representa? Sim! A área da região D (circulo de raio 1)!

∬ S -   r o t   F → ∙ n →   d S = π 1 2 =

π

Resposta

  2. r o t   F → = x z e x y z - x e x y ,   y e y x - y z e x y z ,   - 1
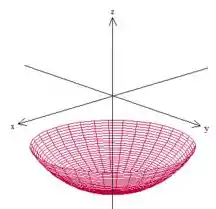
  3. O fluxo de F → através de S é π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê