UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 2.4
2.4. Qual o valor da área limitada entre os gráficos de e ?
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos que obter a área limitada entre as curvas e
E aí? Como fazemos isso? 🤔
Para obter essa área, podemos calcular a integral dessa região através de uma integral dupla.
Primeiramente, podemos esboçar a região que vamos obter e aplicar as variáveis nos limites de integração.
Para calcular a área, a função de integração deve ser .
Bora ver como é na prática? 😉
Passo 2
Primeiro vamos esboçar a região que temos que integrar com a função e
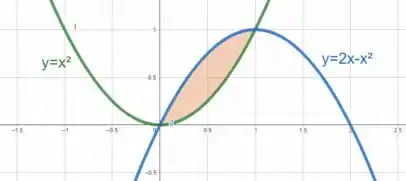
Assim, podemos ver que a região está limitada superiormente pela curva e inferiormente pela curva .
Já em a região tem que variar entre duas constantes já que já consideramos as funções em .
Portanto vemos que varia entre e , que os pontos onde as curvas se cruzam.
Montando nossa integral, temos
Integrando em , temos
Integrando o resultado em função de
Aplicando os limites de integração
Sacou como faz? Responde Aí! 😉
