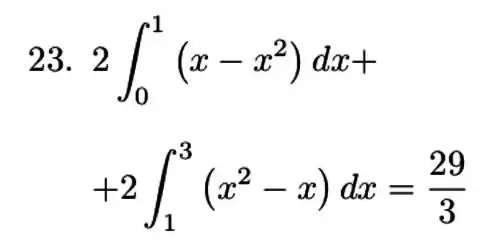Passo 1
Vamos dar uma olhada em como fica o gráfico dessa função. Lembrando que assume a forma ao lado esquerdo do eixo e no lado direito.
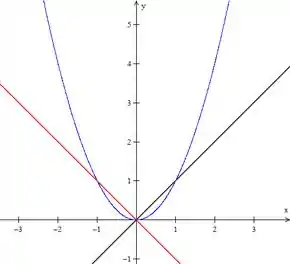
Passo 2
Primeiro vamos determinar o ponto de encontro das curvas.
Vamos precisar calcular a área entre , é maior que . Então
E depois entre e que é o limite do nosso exercício.
Pelo gráfico, podemos ver que essa é uma função simétrica, então para determinar a área entre as curvas basta que façamos o dobro da área de um dos lados.
Então a área total é:
Passo 3
Integrando, vamos ficar com
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x