Passo 1
Bom, para esboçar essa curva não tem muito segredo. Escolha alguns pontos entre os limites que o exercício escolheu e veja o comportamento que vai apresentar.
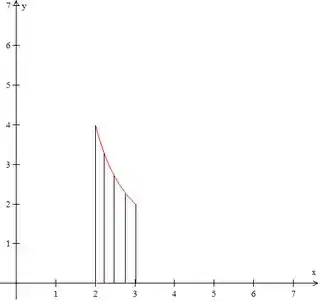
Passo 2
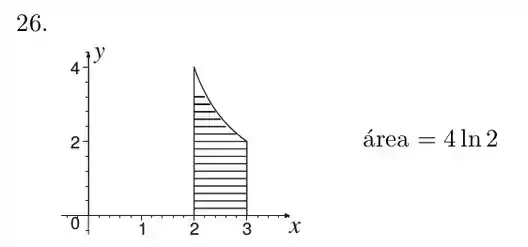
Agora, para determinar a área dessa região, precisamos fazer a integral da curva com os limites de integração que o próprio exercício forneceu.
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x