Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 154123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

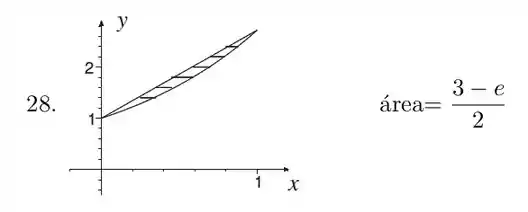
Precisamos começar encontrando e equação da reta que passa pelos pontos 0,1 e 1 , e .  

Supondo uma reta

y = a x + b

Então quando x = 0 ,   y = 1

1 = 0 a + b

b = 1

E quando x = 1 , y = e

e = a + 1

a = e - 1

Então nossa equação da reta é

y = e - 1 x + 1

Passo 2

Determinada a reta, precisamos determinar os pontos de encontro para achar nossos limites de integração para cálculo da área

e - 1 x + 1 = e x

Sabemos então que as raízes serão

x = 0

E

x = 1

Passo 3

Com os limites de integração, já podemos montar nossa integral

∫ 0 1 e - 1 x + 1 - e x d x  

e - 1 x 2 2 + x - e x 0 1

e - 1 2 + 1 - e - 0 + 0 + 1

Aplicando os limites de integração

á r e a = 3 - e 2

Resposta

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x