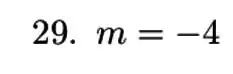![]()
Passo 1
Para começar precisamos encontrar os pontos de intersecção entre as curvas e . Então
Passo 2
Agora vamos montar nossa integral
E fazer a integração
Aplicando os limites
Resposta
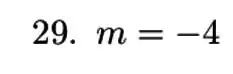
![]()
Para começar precisamos encontrar os pontos de intersecção entre as curvas e . Então
Agora vamos montar nossa integral
E fazer a integração
Aplicando os limites