Passo 1
Para achar essa reta , vamos modelar a reta por e aplicar que a derivada da função vale o coeficiente da função no ponto tratado, , com
Assim, o coeficiente angular será
Com todas essas informações, aplicamos o ponto da reta para descobrir o valor de :
A reta será, portanto, .
Passo 2
A gente tem aqui uma região delimitada lateralmente à esquerda pelo eixo e à direita pela interseção dos gráficos. Nessa região, a reta fica por cima do seno (pode chutar algum valor de entre e e você vai comprovar isso). O esboço fica mais ou menos assim então, dado o gráfico de e da reta:
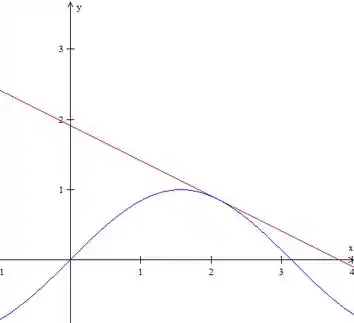
Assim, a área será dada por:
Passo 3
Resolvendo, fica:
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x