UFPB – Cálculo 2 – Listas Prof. Otoniel Nogueira – Lista 04 – Questão 7
Achar a área da região delimitada pelas curvas , com .
Passo 1
Oi, tudo bem?
O problema nos deu essas curvas aqui
, com
E pediu para calcularmos a área da região delimitada por elas! Então nosso primeiro passo é fazer o esboço dessas curvas para ver onde elas se encontram!
Bora começar?
Passo 2
Agora vamos começar fazendo o esboço das curvas e . A primeira é uma reta que passa pela origem e é a abscissa dos quadrantes ímpares. A segunda é um polinômio de terceira ordem que cruza na origem e em :
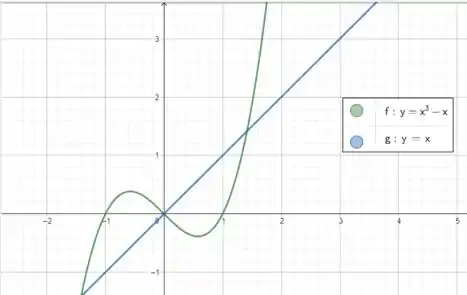
Tudo bem até aqui?
Mas queremos a região com , então a função mais acima é a reta (em azul) e a que está embaixo o polinômio (em verde). E os limites? O limite inferior vemos que é em , o superior é onde as curvas se encontram:
Assim nosso limite de integração fica
tudo bem?
Agora é #partiu integrar
Passo 3
Integrando em temos
Tranquilo? Agora é só aplicar os limites de integração
Beleza? Espero ter ajudado!
