UFPB – Cálculo 2 – Listas Prof. Otoniel Nogueira – Lista 04 – Questão 8
Achar a área da região delimitada pelas curvas ,
Passo 1
Oi, tudo bem?
O problema nos deu essas curvas aqui
,
E pediu para calcularmos a área da região delimitada por elas! Então nosso primeiro passo é fazer o esboço dessas curvas para ver onde elas se encontram!
Bora começar?
Passo 2
Agora vamos começar fazendo o esboço das curvas e . A primeira é uma raiz a segunda é o logaritmo natural de e as duas últimas são retas horizontais
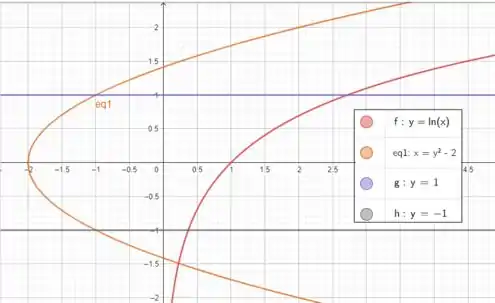
Tudo bem até aqui?
Note que entender essa região como a função em cima menos a de baixo fica pouco complicada. Mas se integrarmos olhando quem está mais à direita menos quem está mais à esquerda fica bem mais fácil! Note que a função em vermelho está sempre mais à direita enquanto a laranja mais à esquerda. E os limites? Vão de até !
tudo bem?
Sendo assim vamos inverter as equações deixando !
Agora é #partiu integrar
Passo 3
Integrando em temos
Tranquilo? Agora é só aplicar os limites de integração
Beleza? Espero ter ajudado!
