Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 347123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Otoniel Nogueira - Lista 04, Questão 15

Achar a área da região delimitada pelas curvas y = x 4 4 , y = 2 x 2 e x + y = 3 com x > 0 .

Passo 1

Eaee!!! Belezinha? Bom... a questão nos pede para determinar a área da região delimitada pelas seguintes curvas:

f x = x 4 4

g x = 2 x 2

x + y = 3 ∴ h x = 3 - x

Lembrando que x > 0 .

De forma gráfica, queremos descobrir essa área:

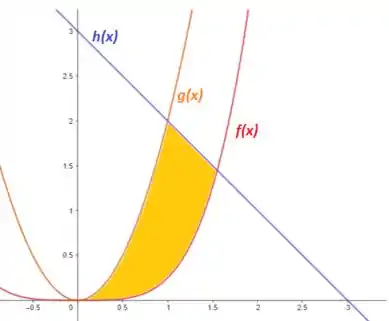
Para descobrirmos essa área A , temos que descobrir os pontos de interseção para conseguirmos encontrar os limites de integração para aplicar da seguinte forma:

A = ∫ f x d x + ∫ g x d x - ∫ h x d x

E aí?? Bora lá??

Passo 2

Bom... Primeiro, vamos encontrar os pontos de interse�o das duas curvas para determinar os limites das integrais.

  • Para h x e g x :

    • h x = g x ∴

    3 - x = 2 x 2 ∴

    2 x 2 + x - 3 = 0 ∴

    x 1 = 1

    x 2 = - 3 2

  • Para h x e f x :

    • h x = f x ∴

    3 - x = x 4 4 ∴

    x 4 4 + x - 3 = 0 ∴

    x = 1,55

  • Para h ( x ) e a o eixo das abscissas:

h x = 0 ∴

x - 3 = 0 ∴

x = 3

Agora vamos descobrir a área!!

Passo 3

Dessa forma, podemos encontrar a área A da seguinte forma:

A = ∫ 0 1 f x d x + ∫ 1 3 g x d x - ∫ 0 1,55 f x d x ∴

A = ∫ 0 1 x 4 4 d x + ∫ 1 3 2 x 2 d x - ∫ 0 1 , 55 3 - x d x ∴

A = x 5 5 1 0 + 2 x 3 3 3 1 - 3 x - x 2 2 1 , 55 0 ∴

A = 1 5 + 52 3 - 3,45 ∴

A = 14,08

Entendeu direitinho? Responde aee ;)

Resposta

A = 14,08

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x