UFSC, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFSC - Lista 2.1 - Áreas entre curvas, Questão P1d
Em cada item, determine a área da região sombreada.
Passo 1
Fala, galera! Vamos resolver essa questão!
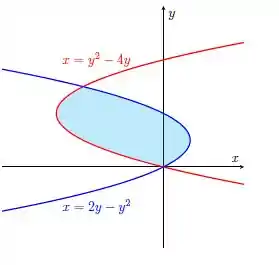
O enunciado pediu pra gente determinar a área entre as curvas de e , que é a nossa área em azul. Repare que as funções são colocada em relação a , então vamos ter uma integral de área em relação a .
Os limites horizontais são definidos pelas duas curvas e os limites verticais vão ser definidos pelas constantes, nos pontos de interseção entre as curvas.
Verificando os limites verticais, vamos ter os limites de integração da região, que vai ser dada pela diferença entre a função que está a direita e a função que está a esquerda, ou seja:
Onde, nesse caso, e .
Vamos lá!
Passo 2
Vamos começar descobrindo o ponto onde as curvas se interseptam lá em cima, fazendo:
Então, os gráficos se tocam em . Como a gente pode ver no gráfico, as curvas também se tocam na origem, ou seja, em . Assim, nossos limites estão no intervalo .
Passo 3
Montando nossa integral de área:
Com e , temos:
Usando a regrinha da potência para integrar (), vamos obter:
Aplicando os limites de integração:
Valeu, galera! Até a próxima! 😉