P-REC – Cálculo 1 – USP – 2022 – Questão 3
Para cada , seja a área delimitada pelas curvas e , com .
a) Calcule .
b) Determine para que seja mínima.
Passo 1
Bom galera.. nessa questão temos que calcular a área delimitada por duas funções.
Nesse caso temos:
e entre .
Para calcular a área delimitada entre funções, nós temos que fazer:
Onde tem que ser maior que no intervalo .
O lance aqui é você entender que é uma função que é sempre menor que até . Após isso, será maior que .
Vou colocar um desenho aqui que deixa isso claro.
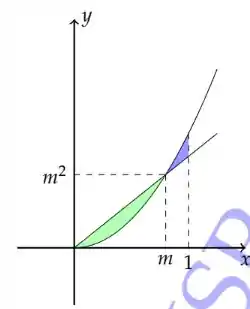
Portanto, para calcular a área em verde, fazemos:
E para calcular a área em azul, fazemos:
E então somamos essas duas áreas.
Passo 2
Calculando a área 1, teremos:
Substituindo os limites, temos:
Passo 3
Já a área 2 será:
Substituindo os limites, temos:
Dessa forma, a área total será:
Passo 4
Para determinar o que nos dá a área mínima, só precisamos derivar a função área e igualar a zero.
Que racionalizando, resulta em:
Como precisa estar entre e , teremos então:
Resposta
a)
b)