Calcule a área do conjunto de todos os pontos tais que (coordenadas polares).
Passo 1
Eaee!!! Belezinha? Bom... antes de tudo, vamos esboçar as duas curvas no plano polar:
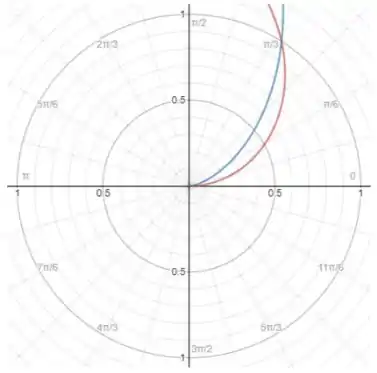
Onde a curva vermelha é e a azul é .
Bom... devemos saber que a área de uma curva polar em um intervalo , é dada por:
Sabendo disso, devemos pegar curva da maior área (vermelha) e subtrair pela curva de menor área (azul)!!
E aí? Bora lá aplicar?
😉
Passo 2
Pela figura, vemos que as curvas se cruzam em e , que são os nossos intervalos de integração!
Nesse sentido, temos:
Resolvendo a integral, temos:
Entendeu direitinho? Responde aee ;)
