UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Integrais, Questão 3.5
3.5. Calcule a área entre as curvas e . Faça um esboço da situação.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nosso objetivo nesse problema é obter a área da região limitada pelas curvas e .
Tem alguma ideia do que fazer? 🤔
Para obter a área entre as duas curvas, podemos usar uma integral dupla do tipo
Então para definir os limites de integração, temos que esboçar as curvas e obter a região.
Bora lá! 👀
Passo 2
As curvas e são paraboloides dadas por
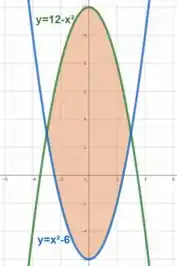
Perceba que a região é limitada superiormente pela curva verde e inferiormente pela curva azul .
Assim, temos que e .
Para obter a variação de , vamos igualar as duas equações
Tranquilo até aqui? 😉
Passo 3
Montando nossa integral com os limites de integração que encontramos, temos
Integrando com relação a
Integrando o resultado em função de ...
Aplicando os limites de integração
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
