UFU, Sem Campus, Cálculo 1, Listas de C1 - Profº Rafael Rossato - Integrais com coordenadas polares, Questão 3a
Calcule a área da intersecção das regiões limitadas pelas curvas dadas em coordenadas polares.
- e
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá duas equações dadas em coordenadas polares:
Sabendo disso, a questão nos pede para calcularmos a área da intersecção das regiões limitadas pelas curvas dadas.
Para isso, primeiramente devemos descobrir onde elas se intersectam. Nesse sentido, teremos os nossos intervalos de integração.
Depois, para descobrir a área, devemos lembrar da seguinte fórmula:
Que nada mais é do que a área para coordenadas polares.
E aí? Bora lá aplicar?
😉
Passo 2
Então... igualando as duas equações para descobrir onde elas se intersectam, temos:
Pelo círculo trigonométrico, vemos que e .
Plotando as duas curvas, temos:
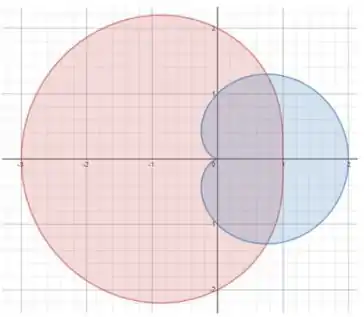
Para fazer o cálculo da área de intersecção, precisamos calcular uma área relativa apenas a um e outra para ficar fácil de calcular, nesse caso.
Se chamarmos a área da esquerda de e a área da direita de , usaremos para o intervalo e para , o intervalo .
Dessa forma, vamos ter uma imagem assim:
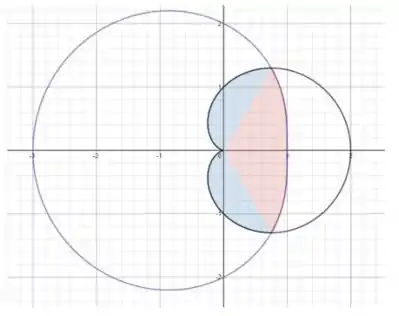
Passo 3
Note que a imagem é simétrica em relação ao eixo .
Dessa forma, podemos multiplicar somente uma das partes, usar a metade do intervalo e depois multiplicar por , assim:
E
Agora vamos resolver nossas integrais!!
Passo 4
Para , temos:
Sabendo que , temos:
Para , temos:
Sabendo que , temos:
Dessa forma, somando as duas integrais, temos:
Entendeu direitinho? Responde aee ;)
