Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 124123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

Calcule a área da região:

R = x , y   ϵ   R 2 x 4 - x ≤ y ≤ x e 2 x ,     x   ϵ   1,2

Passo 1

Cara, a integral já está dada, vai ser a área indo de x 4 - x até x e 2 x , com x variando de 1 a 2 :

A = ∫ a b f x - g x d x = ∫ 1 2 x e 2 x d x - ∫ 1 2 x 4 - x d x

Apenas para podermos visualizar melhor o que estamos calculando, resolvi colocar o gráfico abaixo

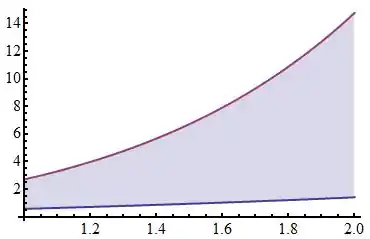
Pronto! Queremos calcular a área marcada no gráfico!

Vou resolver uma integral de cada vez.

∫ 1 2 x 4 - x d x

Essa aí pede uma substituição simples, mas que simplifica muito:

u = 4 - x → d u = - d x

x = 4 - u → d x = - d u

u i n f = 4 - 1 = 3   ; u s u p = 4 - 2 = 2

∫ 1 2 x 4 - x d x = ∫ 3 2 4 - u u - d u = ∫ 3 2 u - 4 u d u = ∫ 3 2 u - 4 u d u

= u 3 2 3 2 - 4 u 1 2 1 2 [ 2 3 = 2 2 3 2 3 - 8 2 1 2 - 2 3 3 2 3 - 8 3 1 2

= 2 4 3 - 8 - 3 2 - 8

= 6 3 - 20 2 3

Passo 2

A outra agora, precisamos resolver por partes. Vamos só resolver a integral para depois botar os limites de integração. E vamos escolher, pelo LIATE, u = x e então e 2 x d x = d v . Substituindo na fórmula da integração por partes, teremos:

u = x → d u = d x

d v = e 2 x d x → v = e 2 x 2

∫ x e 2 x   d x = x e 2 x 2 - ∫ e 2 x 2 d x

Resolvendo a integral, chegamos em:

∫ x e 2 x   d x = x e 2 x 2 - e 2 x 4

= e 2 x 2 x - 1 2

Assim, jogando os limites de integração:

e 2 x 2 x - 1 2 [ 2 1 = e 4 2 2 - 1 2 - e 2 2 1 - 1 2

= e 4 2 3 2 - e 2 2 1 2

= 3 e 4 - e 2 4

Passo 3

Assim, juntando as duas integrais:

∫ 1 2 x e 2 x d x - ∫ 1 2 x 4 - x d x

= 3 e 4 - e 2 4 - 6 3 - 20 2 3

= 3 e 4 - e 2 4 - 6 3 + 20 2 3 u . a .  

Resposta

A = 3 e 4 - e 2 4 - 6 3 + 20 2 3 u . a .  

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x