Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 228123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

Calcule a área da região limitada pelas curvas y = x 2 + 1   e y = | 2 x | . Faça um esboço da região.

Passo 1

O enunciado nos dá duas curvas:

y = x 2 + 1

y = | 2 x |

O enunciado nos pede para esboçar a área limitada por essas curvas e calculá-la.

Passo 2

Para esboçar as curvas, vamos, primeiro entender melhor as funções dadas:

y = x 2 + 1 → y 2 = x 2 + 1 → y 2 - x 2 = 1

Como y = x 2 + 1 → y ≥ 0 . Sendo assim, y 2 - x 2 = 1 é a parte superior de uma hipérbole.

(Lembre que x 2 - y 2 = 1 é a “hipérbole clássica”. Então, y 2 - x 2 = 1 é a hipérbole “em pé” – invertemos x e y em relação à “equação clássica” da hipérbole).

y ' = 1 2 ⋅ 1 x 2 + 1 ⋅ 2 x = x x 2 + 1 → x = 0   é ponto crítico

y ' ' = 1 ⋅ x 2 + 1 - x ⋅ 1 2 ⋅ 1 x 2 + 1 . 2 x x 2 + 1 = 1 x 2 + 1 3 2 > 0 → y   côncava para cima

Logo, x = 0 é ponto de mínimo absoluto. y 0 = 1 .

y = 2 x = 2 x ,     x ≥ 0 - 2 x ,             x ≤ 0

Agora que já podemos esboçar as funções, o próximo passo é igualar as suas equações para acharmos os pontos que elas se interceptam.

Depois, calcularemos a área da região limitada por elas através de integrais.

Passo 3

Igualando as funções:

x 2 + 1 = 2 x → x 2 + 1 = 4 x 2 → 3 x 2 - 1 = 0

x 1 = 1 3 ,       x 2 = - 1 3

Esboço da região R :

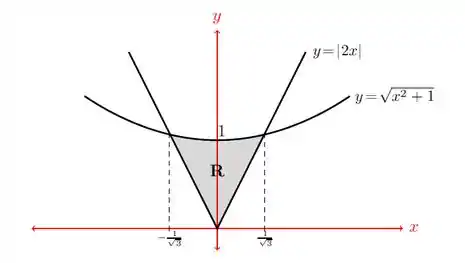
Pela simetria, podemos dizer que a área de R é:

2 ∫ 0 1 3 x 2 + 1 - 2 x d x = 2 ∫ 0 1 3 x 2 + 1   d x - 2 x 2 0 1 3 =

= 2 ∫ 0 1 3 x 2 + 1   d x - 2 3

Passo 4

Vamos calcular a integral: ∫ 0 1 3 x 2 + 1 d x .

Como aparece a expressão x 2 + a 2 , vamos tentar a substituição trigonométrica:

x = tg ⁡ θ ,     d x = sec 2 ⁡ θ d θ         - π 2 ≤ θ ≤ π 2

Mudando os limites de integração:

x = 0 → tg ⁡ θ = 0 → θ = 0

x = 1 3 = 3 3 → tg ⁡ θ = 3 3 → θ = π 6

Aplicando:

∫ 0 π 6 tg 2 ⁡ θ + 1 sec 2 ⁡ θ d θ = ∫ 0 π 6 sec 2 ⁡ θ ⋅ sec 2 ⁡ θ d θ =

= ∫ 0 π 6 sec 3 ⁡ θ d θ = ∫ 0 π 6 1 + tg 2 ⁡ θ ⋅ sec ⁡ θ d θ =

= ∫ 0 π 6 sec ⁡ θ d θ + ∫ 0 π 6 tg 2 ⁡ θ sec ⁡ θ d θ

Passo 5

Resolvendo a segunda integral por partes:

u = tg ⁡ θ → d u = sec 2 ⁡ θ d θ

d v = tg ⁡ θ sec ⁡ θ d θ → v = sec ⁡ θ

∫ 0 π 6 sec 3 ⁡ θ d θ = ∫ 0 π 6 sec ⁡ θ d θ + tg ⁡ θ sec ⁡ θ 0 π 6 - ∫ 0 π 6 sec 3 ⁡ θ d θ

Calculando:

∫ 0 π 6 sec 3 ⁡ θ d θ = 1 2 ln ⁡ | tg ⁡ θ + sec ⁡ θ | + tg ⁡ θ sec ⁡ θ 0 π 6 =

= 1 2 ln ⁡ 3 3 + 2 3 + 3 3 ⋅ 2 3 - 0 + 0 = 1 2 ln ⁡ 3 + 1 3

Substituindo na expressão inicial:

2 ∫ 0 1 3 x 2 + 1 d x - 2 3 =

= ln ⁡ 3 + 2 3 - 2 3 = ln ⁡ ( 3 1 2 ) = 1 2 ln ⁡ ( 3 )

OBS:

Nesse problema, o enunciado nos pediu explicitamente que teríamos que esboçar a região entre as curvas. Portanto, para fazer isso, tivemos que usar conceitos de derivada primeira e derivada segunda para acharmos a concavidade, ponto de mínimo, etc.

É bom estar com esses conceito frescos na hora da prova. Além disso, é bom saber equações de algumas curvas conhecidas:

y = a x + b   ( reta )

y = a x 2 + b x + c   parábola

x - a 2 + y - b 2 = r 2   ( círculo )

x - x 0 2 a 2 + y - y 0 2 b 2 = 1   ( elipse )

x - x 0 2 a 2 - y - y 0 2 b 2 = 1   ( hipérbole )

Resposta

A área é da região é igual a 1 2 ln ⁡ ( 3 ) .

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x