UFCG, Sem Campus, Cálculo Diferencial e Integral II, 1º Estágio - 2022.1, Questão 1
Calcule a área da região do plano compreendida entre as seguintes curvas:
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a área da região entre as curvas e , com variando de a.
Reparou que a gente tem uma função de ? Dessa forma, é definida por funções e é definida em um intervalo (números). Quê que isso nos lembra? Região do Tipo II, certo? Porque uma região do tipo é exatamente isso, é limitada por curvas e é limitada por constantes. Ou seja:
No nosso caso, as constantes e seriam e . E as curvas seriam e . No gráfico isso fica assim:
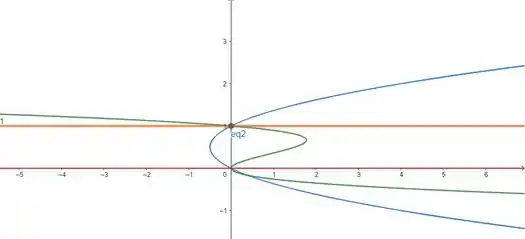
A curva em azul é e em verde temos , elas limitam nossa região horizontalmente. Em vermelho e laranja, temos e , respectivamente, que limitam nossa região verticalmente. Escrevendo essa região na forma integral, vamos ter a área:
Então, vamos calcular essa integral para encontrar a área .
Vamos lá!
Passo 2
Vamos calcular nossa integral:
Integrando primeiro em relação a , temos:
Agora vamos aplicar os intervalos de integração em :
Agora vamos integrar em relação a , usando a regrinha da potência ():
Simplificando as frações:
Agora aplicando os limites de integração em :
E encontramos nossa área.
Valeu, galera! Até a próxima! 😉