Calcule a área da região
Passo 1
A primeira coisa a fazer é esboçar a região.
Vamos começar traçando a parábola , que é bem tranquila:
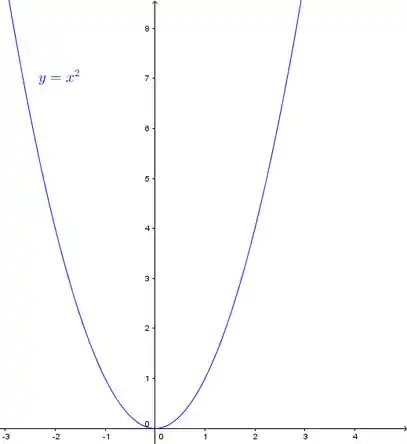
Acrescentando a parábola :
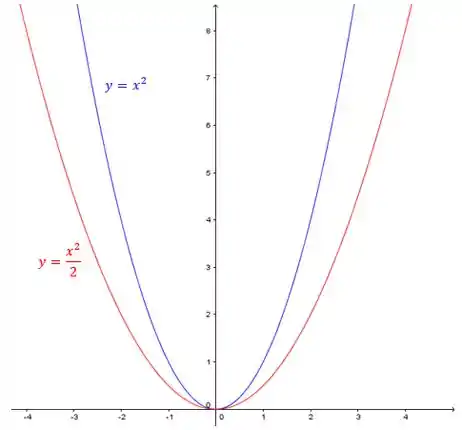
Pra finalizar, a reta :
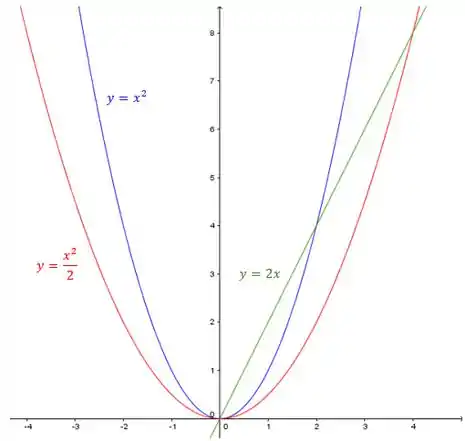
Temos que , então a região é:
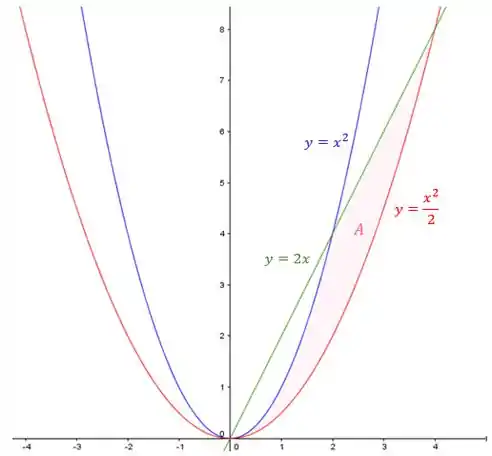
Passo 2
Vejamos onde as curvas se interceptam pra poder montar nossas integrais.
- As 3 curvas se encontram na origem.
- A reta cruza com a parábola em :
- A reta cruza com a parábola em :
Então, olhando a figura, temos que a área de vai ser:
Passo 3
Firmeza, agora só nos resta calcular essas integrais:
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x