UFPB – Cálculo 2 – Listas Prof. Otoniel Nogueira – Lista 04 – Questão 2
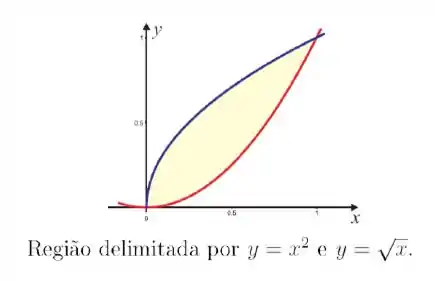
Calcule a área da região situada entre as curvas
Passo 1
Oi, tudo bem?
Vamos calcular essa área aqui
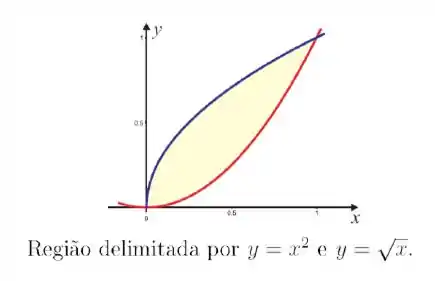
Quando integramos procuramos a função que está mais em cima e a que está mais embaixo. No nosso caso a função em azul está sempre em cima e a vermelha embaixo! Isso significa que não precisamos dividir em duas (ou mais) integrais!
Mas qual será nosso limite de integração? Temos que o ponto de encontro mais à esquerda é , ok, temos o limite inferior! E o superior? Precisamos achar!
Então aqui atenção: vamos começar encontrando o limite superior de integração, onde as curvas se encontram, e depois é partiu integrar!
Bora começar?
Passo 2
Onde elas se encontram:
Elevando tudo ao quadrado temos
Temos duas raízes: e
Beleza? Assim nosso limite de integração é
Tudo bem até aqui? Agora é partiu integração!
Passo 3
Integrando temos
Agora é só aplicar os limites de integração
Beleza? Espero ter ajudado!